
已知函數(shù) .
.
(1)若 的定義域和值域均是
的定義域和值域均是 ,求實數(shù)
,求實數(shù) 的值;
的值;
(2)若 在區(qū)間
在區(qū)間 上是減函數(shù),且對任意的
上是減函數(shù),且對任意的 ,都有
,都有 ,求實數(shù)
,求實數(shù) 的取值范圍;
的取值范圍;
(3)若 ,且對任意的
,且對任意的 ,都存在
,都存在 ,使得
,使得 成立,求實數(shù)
成立,求實數(shù) 的取值范圍.
的取值范圍.
(1)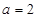 ;(2)
;(2)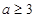 ;(3)
;(3) .
.
解析試題分析:(1)先利用二次函數(shù)的性質(zhì)確定函數(shù) 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為 ,故
,故 在
在 單調(diào)遞減,然后由定義域與值域列出等式關(guān)系,從而求解即可;(2)由(1)可知
單調(diào)遞減,然后由定義域與值域列出等式關(guān)系,從而求解即可;(2)由(1)可知 ,初步確定
,初步確定 的取值范圍
的取值范圍 ,然后確定
,然后確定 時函數(shù)
時函數(shù) 的最大值
的最大值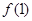 ,從中求解不等式組
,從中求解不等式組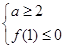 即可;(3)將“對任意的
即可;(3)將“對任意的 ,都存在
,都存在 ,使得
,使得 成立”轉(zhuǎn)化為
成立”轉(zhuǎn)化為 時,
時,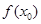 的值域包含了
的值域包含了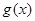 在
在 的值域,然后進行分別求
的值域,然后進行分別求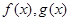 在
在 的值域,從集合間的包含關(guān)系即可求出
的值域,從集合間的包含關(guān)系即可求出 的取值范圍.
的取值范圍.
試題解析:(1)∵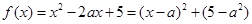
∴ 在
在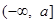 上單調(diào)遞減,又
上單調(diào)遞減,又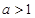 ,∴
,∴ 在
在 上單調(diào)遞減,
上單調(diào)遞減,
∴ ,∴
,∴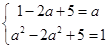 ,∴
,∴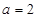 4分
4分
(2)∵ 在區(qū)間
在區(qū)間 上是減函數(shù),∴
上是減函數(shù),∴ ,∴
,∴
∴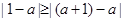 ,
,
∴ 時,
時,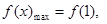
又∵對任意的 ,都有
,都有 ,
,
∴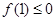 ,即
,即 ,也就是
,也就是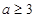
綜上可知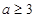 8分
8分
(3)∵ 在
在 上遞增,
上遞增, 在
在 上遞減,
上遞減,
當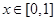 時,
時,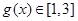 ,
,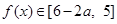
∵對任意的 ,都存在
,都存在 ,使得
,使得 成立
成立
∴
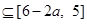
∴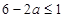 ,所以
,所以 13分
13分
考點:1.二次函數(shù)圖像與性質(zhì);2.函數(shù)的單調(diào)性;3.函數(shù)與方程的問題.


 優(yōu)加精卷系列答案
優(yōu)加精卷系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù) 的定義域是
的定義域是 ,對于任意的
,對于任意的 ,有
,有 ,且當
,且當 時,
時, .
.
(1)求 的值;
的值;
(2)判斷函數(shù)的奇偶性;
(3)用函數(shù)單調(diào)性的定義證明函數(shù) 為增函數(shù);
為增函數(shù);
(4)若 恒成立,求實數(shù)
恒成立,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
近日,國家經(jīng)貿(mào)委發(fā)出了關(guān)于深入開展增產(chǎn)節(jié)約運動,大力增產(chǎn)市場適銷對路產(chǎn)品的通知,并發(fā)布了當前國內(nèi)市場185種適銷工業(yè)品和42種滯銷產(chǎn)品的參考目錄.為此,一公司舉行某產(chǎn)品的促銷活動,經(jīng)測算該產(chǎn)品的銷售量P萬件(生產(chǎn)量與銷售量相等)與促銷費用x萬元滿足 (其中
(其中 ,a為正常數(shù)).已知生產(chǎn)該產(chǎn)品還需投入成本10+2P萬元(不含促銷費用),產(chǎn)品的銷售價格定為
,a為正常數(shù)).已知生產(chǎn)該產(chǎn)品還需投入成本10+2P萬元(不含促銷費用),產(chǎn)品的銷售價格定為 元/件.
元/件.
(1)將該產(chǎn)品的利潤y萬元表示為促銷費用x萬元的函數(shù);
(2)促銷費用投入多少萬元時,廠家的利潤最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) .
.
(Ⅰ)若 ,試判斷
,試判斷 在定義域內(nèi)的單調(diào)性;
在定義域內(nèi)的單調(diào)性;
(Ⅱ) 當 時,若
時,若 在
在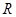 上有
上有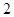 個零點,求
個零點,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
我國是水資源較貧乏的國家之一,各地采用價格調(diào)控等手段來達到節(jié)約用水的目的,某市每戶每月用水收費辦法是:水費=基本費+超額費+定額損耗費.且有如下兩條規(guī)定:
①若每月用水量不超過最低限量 立方米,只付基本費10元加上定額損耗費2元;
立方米,只付基本費10元加上定額損耗費2元;
②若用水量超過 立方米時,除了付以上同樣的基本費和定額損耗費外,超過部分每立方米加付
立方米時,除了付以上同樣的基本費和定額損耗費外,超過部分每立方米加付 元的超額費.
元的超額費.
解答以下問題:(1)寫出每月水費 (元)與用水量
(元)與用水量 (立方米)的函數(shù)關(guān)系式;
(立方米)的函數(shù)關(guān)系式;
(2)若該市某家庭今年一季度每月的用水量和支付的費用如下表所示:
| 月份 | 用水量(立方米) | 水費(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
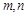 的值.
的值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù) 對任意
對任意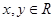 ,都有
,都有 ,當
,當 時,
時,
(1)求證: 是奇函數(shù);
是奇函數(shù);
(2)試問:在 時
時  ,
, 是否有最大值?如果有,求出最大值,如果沒有,說明理由.
是否有最大值?如果有,求出最大值,如果沒有,說明理由.
(3)解關(guān)于x的不等式
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)f(x)= .
.
(1)求函數(shù)f(x)的定義域;
(2)設(shè)α是第四象限的角,且tan α=- ,求f(α)的值.
,求f(α)的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com