
已知函數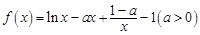 .
.
(1)設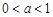 ,試討論
,試討論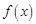 單調性;
單調性;
(2)設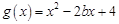 ,當
,當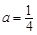 時,若
時,若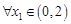 ,存在
,存在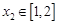 ,使
,使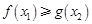 ,求實數
,求實數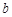 的
的
取值范圍.
(1)當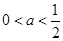 時,
時,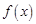 在
在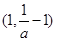 上是增函數,在
上是增函數,在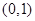 和
和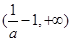 上是減函數;當
上是減函數;當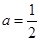 時,
時,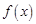 在
在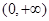 上是減函數;當
上是減函數;當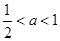 時,
時,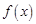 在
在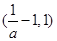 上是增函數,在
上是增函數,在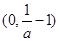 和
和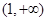 上是減函數;(2)
上是減函數;(2)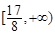 .
.
【解析】
試題分析:(1)先求出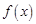 的導數,
的導數,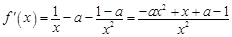 ,然后在
,然后在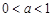 的范圍內討論
的范圍內討論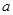 的大小以確定
的大小以確定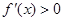 和
和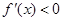 的解集;(2)
的解集;(2)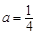 時,代入結合上問可知函數
時,代入結合上問可知函數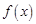 在在
在在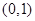 上是減函數,在
上是減函數,在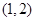 上是增函數,即在
上是增函數,即在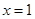 取最小值,若
取最小值,若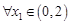 ,存在
,存在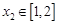 ,使
,使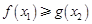 ,即存在
,即存在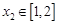 使得
使得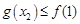 .從而得出實數
.從而得出實數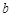 的取值范圍.注意
的取值范圍.注意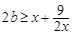 不能用基本不等式,因為
不能用基本不等式,因為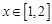 等號取不到,實際上
等號取不到,實際上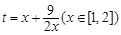 為減函數.所以其值域為
為減函數.所以其值域為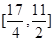 ,從而
,從而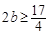 ,即有
,即有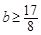 .
.
試題解析:(1)函數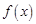 的定義域為
的定義域為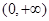 ,
,
因為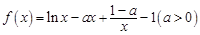 ,所以
,所以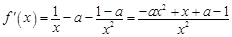 ,
,
令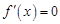 ,可得
,可得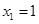 ,
,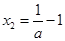 ,
,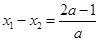 2分
2分
①當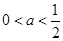 時,由
時,由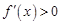 可得
可得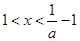 ,故此時函數
,故此時函數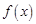 在
在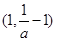 上是增函數.
上是增函數.
同樣可得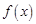 在
在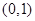 和
和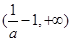 上是減函數.
4分
上是減函數.
4分
②當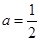 時,
時,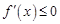 恒成立,故此時函數
恒成立,故此時函數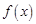 在
在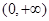 上是減函數.
6分
上是減函數.
6分
③當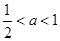 時,由
時,由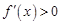 可得
可得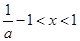 ,故此時函數
,故此時函數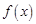 在
在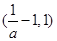 上是增函數,
上是增函數,
在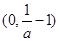 和
和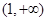 上是減函數;
8分
上是減函數;
8分
(2)當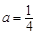 時,由(1)可知
時,由(1)可知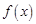 在
在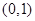 上是減函數,在
上是減函數,在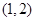 上是增函數,
上是增函數,
所以對任意的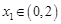 ,有
,有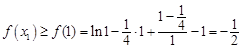 ,
,
由條件存在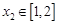 ,使
,使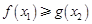 ,所以
,所以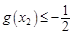 ,
12分
,
12分
即存在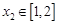 ,使得
,使得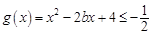 ,
,
即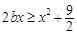 在
在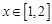 時有解,
時有解,
亦即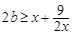 在
在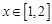 時有解,
時有解,
由于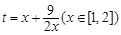 為減函數,故其值域為
為減函數,故其值域為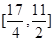 ,
,
從而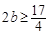 ,即有
,即有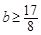 ,所以實數
,所以實數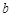 的取值范圍是
的取值范圍是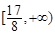 .
16分
.
16分
考點:1.常見函數的導數;2.利用導數研究函數的單調性;3.利用函數單調性求最值.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2007-2008學年浙江省杭州二中高三(上)10月月考數學試卷(理科)(解析版) 題型:解答題
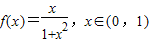 .
. ;
; 的最小值.
的最小值.查看答案和解析>>
科目:高中數學 來源:2010年四川省眉山市高考數學二模試卷(文科)(解析版) 題型:解答題
 .
. 的值域.
的值域.查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省天水市高三第二次學段考試理科數學試卷(解析版) 題型:解答題
(本小題滿分12分) 已知函數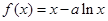 ,
,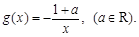
(1)設函數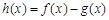 ,求函數
,求函數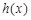 的單調區間;
的單調區間;
(2)若在區間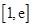 (
(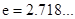 )上存在一點
)上存在一點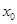 ,使得
,使得
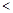
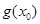 成立,求
成立,求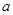 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山西省高三年級第四次四校聯考文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)已知函數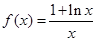 .
.
(1)設a>0,若函數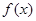 在區間
在區間 上存在極值,求實數a的取值范圍;
上存在極值,求實數a的取值范圍;
(2)如果當x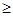 1時,不等式
1時,不等式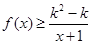 恒成立,求實數k的取值范圍.
恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三5月月考理科數學試卷(解析版) 題型:解答題
已知函數 與
與
(1)設直線 分別相交于點
分別相交于點 ,且曲線
,且曲線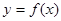 和
和 在點
在點 處的切線平行,求實數
處的切線平行,求實數 的值;
的值;
(2) 為
為 的導函數,若對于任意的
的導函數,若對于任意的 ,
, 恒成立,求實數
恒成立,求實數 的最大值;
的最大值;
(3)在(2)的條件下且當 取
取 最大值的
最大值的 倍時,當
倍時,當 時,若函數
時,若函數 的最小值恰為
的最小值恰為 的最小值,求實數
的最小值,求實數 的值
的值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com