Question

【題目】已知橢圓C的標準方程為：，該橢圓經(jīng)過點P（1，），且離心率為．

（Ⅰ）求橢圓的標準方程；

（Ⅱ）過橢圓長軸上一點S（1，0）作兩條互相垂直的弦AB、CD．若弦AB、CD的中點分別為M、N，證明：直線MN恒過定點．

Answer 1

【答案】（1）（2）

【解析】

（Ⅰ）由已知條件推導出，e=，由此能求出橢圓方程．

（Ⅱ）設(shè)直線AB的方程為x=my+s，m≠0，則直線CD的方程為x=﹣，聯(lián)立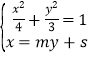，得M（），將M的坐標中的m用﹣代換，得CD的中點N（），從而得到直線MN的方程為x﹣y=，由此能證明直線MN經(jīng)過定點（）．

（Ⅰ）解：∵點P（1，）在橢圓上，∴，又∵離心率為，∴e=，∴a=2c，∴4a2﹣4b2=a2，解得a2=4，b2=3，

∴橢圓方程為．

（Ⅱ）證明：設(shè)直線AB的方程為x=my+s，m≠0，則直線CD的方程為x=﹣，聯(lián)立，得（3m2+4）y2+6smy+3s2﹣12=0，

設(shè)A（x1，y1），B（x2，y2），則，，∴x1+x2=（my1+s）（my2+s）=m2y1y2+ms（y1+y2）+s2=，

由中點坐標公式得M（，﹣），將M的坐標中的m用﹣代換，得CD的中點N（，）

∴直線MN的方程為x﹣y=，m≠±1，令y=0得：x=，∴直線MN經(jīng)過定點（），

當m=0，±1時，直線MN也經(jīng)過定點（），綜上所述，直線MN經(jīng)過定點（）．

當時，過定點