
【題目】如圖,已知菱形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() .
.

(1)求直線![]() 與平面
與平面![]() 的夾角;
的夾角;
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1) ![]() . (2)
. (2) ![]()
【解析】
設![]() ,以
,以![]() 點為坐標原點,以
點為坐標原點,以![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,過
軸,過![]() 點且平行于
點且平行于![]() 的方向為
的方向為![]() 軸正方向,建立空間坐標系,
軸正方向,建立空間坐標系,
(1)由題意,求出直線![]() 的方向向量,平面
的方向向量,平面![]() 的一個法向量,由向量夾角,即可得到直線與平面夾角;
的一個法向量,由向量夾角,即可得到直線與平面夾角;
(2)先求出平面![]() 的一個法向量
的一個法向量![]() ,由點
,由點![]() 到平面
到平面![]() 的距離
的距離 ,即可求出結果.
,即可求出結果.
設![]() ,因為菱形
,因為菱形![]() 和矩形
和矩形![]() 所在的平面互相垂直,所以易得
所在的平面互相垂直,所以易得![]() 平面
平面![]() ;以
;以![]() 點為坐標原點,以
點為坐標原點,以![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,過
軸,過![]() 點且平行于
點且平行于![]() 的方向為
的方向為![]() 軸正方向,建立空間坐標系,
軸正方向,建立空間坐標系,
(1)由已知得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因為![]() 軸垂直于平面
軸垂直于平面![]() ,
,
因此可令平面![]() 的一個法向量為
的一個法向量為![]() ,又
,又![]() ,
,
設直線![]() 與平面
與平面![]() 的夾角為
的夾角為![]() ,
,
則有 ,
,
即![]() ,
,
所以直線BF與平面ABCD的夾角為![]() .
.
(2)因為![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
 ,令
,令![]() 得
得![]() ,
,
又因為![]() ,
,
所以點![]() 到平面
到平面![]() 的距離
的距離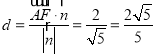 .
.



科目:高中數學 來源: 題型:
【題目】在平面直角坐標![]() 系中,直線
系中,直線![]() 的參數方程為:
的參數方程為:![]() (
(![]() 為參數,
為參數,![]() ),以
),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程
的極坐標方程![]() .
.
(1)①當![]() 時,寫出直線
時,寫出直線![]() 的普通方程;
的普通方程;
②寫出曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() ,設曲線
,設曲線![]() 與直線
與直線![]() 交于點
交于點![]() ,求
,求![]() 最小值.
最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以直角坐標系原點為極點,以
為參數).以直角坐標系原點為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地需要修建一條大型輸油管道通過120公里寬的沙漠地帶,該段輸油管道兩端的輸油站已建好,余下工程只需要在該段兩端已建好的輸油站之間鋪設輸油管道和等距離修建增壓站(又稱泵站)。經預算,修建一個增壓站的工程費用為400萬元,鋪設距離為![]() 公里的相鄰兩增壓站之間的輸油管道費用為
公里的相鄰兩增壓站之間的輸油管道費用為![]() 萬元。設余下工程的總費用為
萬元。設余下工程的總費用為![]() 萬元。
萬元。
(I)試將![]() 表示成關于
表示成關于![]() 的函數;
的函數;
(II)需要修建多少個増壓站才能使總費用![]() 最小?
最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機構為研究學生玩電腦游戲和對待作業量態度的關系,隨機抽取了100名學生進行調查,所得數據如下表所示:
認為作業多 | 認為作業不多 | 總計 | |
喜歡玩電腦游戲 | 25 | 15 | 40 |
不喜歡玩電腦游戲 | 25 | 35 | 60 |
總計 | 50 | 50 | 100 |
(參考公式![]() ,可能用到數據:
,可能用到數據:![]() ,
,![]() ),參照以上公式和數據,得到的正確結論是( )
),參照以上公式和數據,得到的正確結論是( )
A. 有![]() 的把握認為喜歡玩電腦游戲與對待作業量的態度有關
的把握認為喜歡玩電腦游戲與對待作業量的態度有關
B. 有![]() 的把握認為喜歡玩電腦游戲與對待作業量的態度無關
的把握認為喜歡玩電腦游戲與對待作業量的態度無關
C. 有![]() 的把握認為喜歡玩電腦游戲與對待作業量的態度有關
的把握認為喜歡玩電腦游戲與對待作業量的態度有關
D. 有![]() 的把握認為喜歡玩電腦游戲與對待作業量的態度無關
的把握認為喜歡玩電腦游戲與對待作業量的態度無關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,若對于
,若對于![]() 分別為某個三角形的邊長,則稱
分別為某個三角形的邊長,則稱![]() 為“三角形函數”.給出下列四個函數:
為“三角形函數”.給出下列四個函數:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中為“三角形函數”的個數是( )
.其中為“三角形函數”的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 為
為![]() 上任意一點,
上任意一點,![]() 為菱形
為菱形![]() 對角線的交點。
對角線的交點。
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,當四棱錐的體積被平面
,當四棱錐的體積被平面![]() 分成3:1兩部分時,若二面角
分成3:1兩部分時,若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值。
的值。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是網格工作者經常用來解釋網絡運作的蛇形模型:數字1出現在第1行;數字2,3出現在第2行,數字6,5,4(從左至右)出現在第3行;數字7,8,9,10出現在第4行;依此類推,若數字195在第m行從左至右算第n個數字,則![]() 為_______.
為_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形![]() 中,
中,![]() 分別是
分別是![]() 的中點將
的中點將![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 重合于點
重合于點![]() .則下列結論正確的是( )
.則下列結論正確的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值為
的余弦值為![]()
D. 點![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com