
【題目】如圖,在三棱錐![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是以
是以![]() 為斜邊的等腰直角三角形,
為斜邊的等腰直角三角形,![]() ,
,![]() 是線段
是線段![]() 上一點(diǎn).
上一點(diǎn).
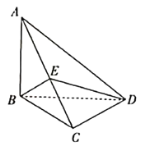
(1)若![]() 為
為![]() 的中點(diǎn),求直線
的中點(diǎn),求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
(2)是否存在點(diǎn)![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,請指出點(diǎn)
?若存在,請指出點(diǎn)![]() 的位置,并加以證明;若不存在,請說明理由.
的位置,并加以證明;若不存在,請說明理由.
【答案】(1)![]() (2)存在,點(diǎn)
(2)存在,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .證明見解析
.證明見解析
【解析】
以B為原點(diǎn)建立空間直角坐標(biāo)系,(1)求出平面BDE的法向量,直線AC的方向向量,求出向量夾角的余弦值的絕對值即為直線![]() 與平面
與平面![]() 所成角的正弦值;(2)先假設(shè)結(jié)論成立,分別求出平面
所成角的正弦值;(2)先假設(shè)結(jié)論成立,分別求出平面![]() 平面
平面![]() 的法向量,由平面
的法向量,由平面![]() 平面
平面![]() 可知兩法向量的數(shù)量積為0,即可求解點(diǎn)E的位置.
可知兩法向量的數(shù)量積為0,即可求解點(diǎn)E的位置.
解:不妨設(shè)![]() ,在平面
,在平面![]() 中作
中作![]() ,以
,以![]() ,
,![]() ,
,![]() 所在的直線為
所在的直線為![]() ,
,![]() ,
,![]() 軸建立如圖所示的空間直角坐標(biāo)系
軸建立如圖所示的空間直角坐標(biāo)系![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)因?yàn)辄c(diǎn)![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),
所以點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
設(shè)![]() 是平面
是平面![]() 的法向量,則
的法向量,則
即
取![]() ,則
,則![]() ,所以平面
,所以平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() .
.
所以
 ,
,
所以直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.
(2)假設(shè)存在點(diǎn)![]() 使得平面
使得平面![]() 平面
平面![]() ,設(shè)
,設(shè)![]() .
.
顯然![]() ,
,![]() .
.
設(shè)![]() 是平面
是平面![]() 的法向量,則
的法向量,則 即
即
取![]() ,則
,則![]() ,
,![]() ,所以平面
,所以平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() .
.
因?yàn)?/span>![]() ,所以點(diǎn)
,所以點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
所以![]() ,
,![]() .
.
設(shè)![]() 是平面
是平面![]() 的法向量,則
的法向量,則 即
即
取![]() ,則
,則![]() ,所以平面
,所以平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() .
.
因?yàn)槠矫?/span>![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() .
.
所以![]() 的值為2,即當(dāng)
的值為2,即當(dāng)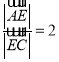 時(shí),平面
時(shí),平面![]() 平面
平面![]() .
.


 課程達(dá)標(biāo)測試卷闖關(guān)100分系列答案
課程達(dá)標(biāo)測試卷闖關(guān)100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關(guān)100分系列答案
全能闖關(guān)100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某單位年會進(jìn)行抽獎活動,在抽獎箱里裝有![]() 張印有“一等獎”的卡片,
張印有“一等獎”的卡片, ![]() 張印
張印
有“二等獎”的卡片, 3張印有“新年快樂”的卡片,抽中“一等獎”獲獎![]() 元, 抽中“二等獎”獲獎
元, 抽中“二等獎”獲獎![]() 元,抽中“新年快樂”無獎金.
元,抽中“新年快樂”無獎金.
(1)單位員工小張參加抽獎活動,每次隨機(jī)抽取一張卡片,抽取后不放回.假如小張一定要將所有獲獎卡片全部抽完才停止. 記![]() 表示“小張恰好抽獎
表示“小張恰好抽獎![]() 次停止活動”,求
次停止活動”,求![]() 的值;
的值;
(2)若單位員工小王參加抽獎活動,一次隨機(jī)抽取![]() 張卡片.
張卡片.
①![]() 記
記![]() 表示“小王參加抽獎活動中獎”,求
表示“小王參加抽獎活動中獎”,求![]() 的值;
的值;
②設(shè)![]() 表示“小王參加抽獎活動所獲獎金數(shù)(單位:元)”,求
表示“小王參加抽獎活動所獲獎金數(shù)(單位:元)”,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了在夏季降溫和冬季供暖時(shí)減少能源損耗,房屋的屋頂和外墻需要建造隔熱層。某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元。該建筑物每年的能源消耗費(fèi)用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關(guān)系:C(x)=![]() 若不建隔熱層,每年能源消耗費(fèi)用為8萬元。設(shè)f(x)為隔熱層建造費(fèi)用與20年的能源消耗費(fèi)用之和。
若不建隔熱層,每年能源消耗費(fèi)用為8萬元。設(shè)f(x)為隔熱層建造費(fèi)用與20年的能源消耗費(fèi)用之和。
(Ⅰ)求k的值及f(x)的表達(dá)式。
(Ⅱ)隔熱層修建多厚時(shí),總費(fèi)用f(x)達(dá)到最小,并求最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)m>0時(shí),若對于區(qū)間[1,2]上的任意兩個(gè)實(shí)數(shù)x1,x2,且x1<x2,都有![]() ,成立,求m的最大值.
,成立,求m的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示的是某池塘中的浮萍蔓延的面積![]() 與時(shí)間
與時(shí)間![]() 月)的關(guān)系
月)的關(guān)系![]() 有以下敘述:
有以下敘述:
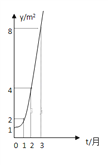
①這個(gè)指數(shù)函數(shù)的底數(shù)是2;
②第5個(gè)月時(shí),浮萍的面積就會超過![]()
③浮萍從![]() 蔓延到
蔓延到![]() 需要經(jīng)過1.5個(gè)月;
需要經(jīng)過1.5個(gè)月;
④浮萍每個(gè)月增加的面積都相等;
⑤若浮萍蔓延到![]() 所經(jīng)過的時(shí)間分別為
所經(jīng)過的時(shí)間分別為![]() 則
則![]() .其中正確的是
.其中正確的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解社會對學(xué)校辦學(xué)質(zhì)量的滿意程度,某學(xué)校決定用分層抽樣的方法從高中三個(gè)年級的家長委員會中共抽取![]() 人進(jìn)行問卷調(diào)查,已知高一、高二、高三、的家長委員會分別有
人進(jìn)行問卷調(diào)查,已知高一、高二、高三、的家長委員會分別有![]() 人,
人,![]() 人,
人,![]() 人.
人.
![]() 求從三個(gè)年級的家長委員會分別應(yīng)抽到的家長人數(shù);
求從三個(gè)年級的家長委員會分別應(yīng)抽到的家長人數(shù);
![]() 若從抽到的
若從抽到的![]() 人中隨機(jī)抽取
人中隨機(jī)抽取![]() 人進(jìn)行調(diào)查結(jié)果的對比,求這
人進(jìn)行調(diào)查結(jié)果的對比,求這![]() 人中至少有一人是高三學(xué)生家長的概率.
人中至少有一人是高三學(xué)生家長的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 。
。
(1)若曲線![]() 與
與![]() 在點(diǎn)
在點(diǎn)![]() 處的切線互相垂直,求
處的切線互相垂直,求![]() 值;
值;
(2)討論函數(shù)![]() 的零點(diǎn)個(gè)數(shù)。
的零點(diǎn)個(gè)數(shù)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(I) 當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II) 當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】四大名著是中國文學(xué)史上的經(jīng)典作品,是世界寶貴的文化遺產(chǎn).某學(xué)校舉行的“文學(xué)名著閱讀月”活動中,甲、乙、丙、丁、戊五名同學(xué)相約去學(xué)校圖書室借閱四大名著《紅樓夢》、《三國演義》、《水滸傳》、《西游記》(每種名著均有若干本),要求每人只借閱一本名著,每種名著均有人借閱,且甲只借閱《三國演義》,則不同的借閱方案種數(shù)為_______.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com