【題目】已知圓
與圓
.
（1）若圓
與圓
外切，求實數(shù)m的值；
（2）在（1）的條件下，若直線l與圓的相交弦長為
且過點
，求直線l的方程.
【答案】（1）
；（2）直線l方程為：
或
【解析】
（1）先根據(jù)圓的方程求出圓心坐標(biāo)和半徑，再由由圓
與圓
外切，可知兩圓心的距離等于兩圓半徑之和，代入數(shù)據(jù)求解即可；
（2）分析可知弦的垂直平分線過圓心，由勾股定理可求出圓心到直線的距離，再由直線l過點
，可設(shè)出直線方程，分斜率存在和不存在兩種情況，求出方程即可.
（1）
，
，
，
，
，
，
圓與圓外切，
，
，
；
（2）由（1）得，圓的方程為
，
設(shè)圓心到直線l的距離
，因為直線l與圓的相交弦長為
，則有
，代入數(shù)據(jù)解得
，
當(dāng)直線l無斜率時：直線方程為.符合題意.
當(dāng)直線l斜率為k時，則直線方程為
，
化為一般形式為
，
則圓心
到直線l的距離
，解得
.
綜上，直線l方程為：或.
周周清檢測系列答案
輕巧奪冠周測月考直通高考系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓C：
1（a＞b＞0）經(jīng)過點（
，1），F（0，1）是C的一個焦點，過F點的動直線l交橢圓于A，B兩點．
（1）求橢圓C的方程
（2）是否存在定點M（異于點F），對任意的動直線l都有kMA+kMB＝0，若存在求出點M的坐標(biāo)，若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)命題p：實數(shù)x滿足x2﹣4ax+3a2＜0（a＞0），命題q：實數(shù)x滿足x2﹣5x+6＜0．
（1）若a＝1，且p∧q為真命題，求實數(shù)x的取值范圍；
（2）若p是q的必要不充分條件，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
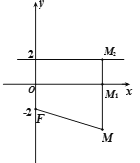
【題目】甲、乙兩位同學(xué)分別做下面這道題目：在平面直角坐標(biāo)系中，動點
到
的距離比到
軸的距離大
，求的軌跡.甲同學(xué)的解法是：解：設(shè)的坐標(biāo)是
，則根據(jù)題意可知
，化簡得
； ①當(dāng)
時，方程可變?yōu)?/span>
；②這表示的是端點在原點、方向為
軸正方向的射線，且不包括原點； ③當(dāng)
時，方程可變?yōu)?/span>
； ④這表示以為焦點，以直線
為準(zhǔn)線的拋物線；⑤所以的軌跡為端點在原點、方向為軸正方向的射線，且不包括原點和以為焦點，以直線為準(zhǔn)線的拋物線. 乙同學(xué)的解法是：解：因為動點到的距離比到軸的距離大. ①如圖，過點
作軸的垂線，垂足為
. 則
.設(shè)直線
與直線的交點為
，則
； ②即動點到直線的距離比到軸的距離大； ③所以動點到的距離與到直線的距離相等；④所以動點的軌跡是以為焦點，以直線為準(zhǔn)線的拋物線； ⑤甲、乙兩位同學(xué)中解答錯誤的是________（填“甲”或者“乙”），他的解答過程是從_____處開始出錯的（請在橫線上填寫① 、②、③、④ 或⑤ ）.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】高二年級舉行一次演講賽共有10位同學(xué)參賽，其中一班有3位，二班有2位，其它班有5位，若采用抽簽的方式確定他們的演講順序，則一班有3位同學(xué)恰好被排在一起（指演講序號相連），而二班的2位同學(xué)沒有被排在一起的概率為：（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列說法正確的是（ ）
A.命題“若
．則a，b中至少有一個不小于1”的逆命題是一個真命題
B.命題“負數(shù)的平方是正數(shù)”是特稱命題
C.命題“設(shè)a，
，若
，則
或
”是一個真命題
D.常數(shù)數(shù)列既是等差數(shù)列也是等比數(shù)列
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】拋物線
的焦點F為圓C：
的圓心．
求拋物線的方程與其準(zhǔn)線方程；
直線l與圓C相切，交拋物線于A，B兩點；
若線段AB中點的縱坐標(biāo)為
，求直線l的方程；
求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，橢圓
：
的左、右焦點分別為
，
軸，直線
交
軸于
點，
，
為橢圓上的動點，
的面積的最大值為1.
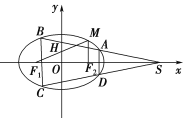
(1)求橢圓的方程；
(2)過點
作兩條直線與橢圓分別交于
且使
軸，如圖，問四邊形
的兩條對角線的交點是否為定點？若是，求出定點的坐標(biāo)；若不是，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】（5分）《九章算術(shù)》“竹九節(jié)”問題：現(xiàn)有一根9節(jié)的竹子，自上而下各節(jié)的容積成等差數(shù)列，上面4節(jié)的容積共3升，下面3節(jié)的容積共4升，則第五節(jié)的容積為（ ）
A. 1升 B. 
升 C. 
升 D. 
升
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com