
【題目】如圖所示,某鎮有一塊空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 。當地鎮政府規劃將這塊空地改造成一個旅游景點,擬在中間挖一個人工湖
。當地鎮政府規劃將這塊空地改造成一個旅游景點,擬在中間挖一個人工湖![]() ,其中
,其中![]() 都在邊
都在邊![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地帶上形成假山,剩下的
地帶上形成假山,剩下的![]() 地帶開設兒童游樂場. 為安全起見,需在
地帶開設兒童游樂場. 為安全起見,需在![]() 的周圍安裝防護網.
的周圍安裝防護網.
(1)當![]() 時,求防護網的總長度;
時,求防護網的總長度;
(2)若要求挖人工湖用地![]() 的面積是堆假山用地
的面積是堆假山用地![]() 的面積的
的面積的![]() 倍,試確定
倍,試確定![]() 的大小;
的大小;
(3)為節省投入資金,人工湖![]() 的面積要盡可能小,問如何設計施工方案,可使
的面積要盡可能小,問如何設計施工方案,可使![]() 的面積最小?最小面積是多少?
的面積最小?最小面積是多少?

【答案】(1)防護網的總長度為![]() (2)
(2)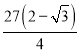
【解析】試題分析:(1)首先根據直角三角形中![]() ,得到
,得到![]() ,結合
,結合![]() ,由余弦定理可求得
,由余弦定理可求得![]() 的值,利用勾股定理證得
的值,利用勾股定理證得![]() ,由此證得三角形
,由此證得三角形![]() 為等邊三角形,從而求出周長.(2) 設
為等邊三角形,從而求出周長.(2) 設![]() ,根據
,根據![]() 的面積是堆假山用地
的面積是堆假山用地![]() 的面積的
的面積的![]() 倍列方程,求得
倍列方程,求得![]() 的值,在
的值,在![]() 中利用正弦定理求得
中利用正弦定理求得![]() 值,兩個值相等,由此求得
值,兩個值相等,由此求得![]() 的值.(3) 在
的值.(3) 在![]() 中,利用正弦定理求得
中,利用正弦定理求得![]() 的值,利用三角形面積公式寫出面積的表達式,并利用三角函數值域來求面積的最小值.
的值,利用三角形面積公式寫出面積的表達式,并利用三角函數值域來求面積的最小值.
試題解析:
(1)![]() 在
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
由余弦定理,得![]() ,
,
![]() ,即
,即![]() ,
, ![]() ,
,
![]() 為正三角形,所以
為正三角形,所以![]() 的周長為
的周長為![]() ,
,
即防護網的總長度為![]() .
.
(2)設![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
在![]() 中,由
中,由![]() ,得
,得![]() ,
,
從而![]() ,即
,即![]() ,由
,由![]() ,
,
得![]() ,
, ![]() ,即
,即![]()
![]() .
.
(3)設![]() ,由(2)知
,由(2)知![]() ,
,
又在![]() 中,由
中,由![]() ,得
,得 ,
,
![]()
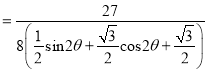
![]() ,
,
![]() 當且僅當
當且僅當![]() ,即
,即![]() 時,
時,
![]() 的面積取最小值為
的面積取最小值為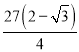
![]() .
.


 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】已知點O為△ABC的外心,角A,B,C的對邊分別滿足a,b,c, (Ⅰ)若3 ![]() +4
+4 ![]() +5
+5 ![]() =
= ![]() ,求cos∠BOC的值;
,求cos∠BOC的值;
(Ⅱ)若 ![]()
![]() =
= ![]()
![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2015﹣2016賽季CBA聯賽中,某隊甲、乙兩名球員在前10場比賽中投籃命中情況統計如下表(注:表中分數 ![]() ,N表示投籃次數,n表示命中次數),假設各場比賽相互獨立.
,N表示投籃次數,n表示命中次數),假設各場比賽相互獨立.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
根據統計表的信息:
(1)從上述比賽中等可能隨機選擇一場,求甲球員在該場比賽中投籃命中率大于0.5的概率;
(2)試估計甲、乙兩名運動員在下一場比賽中恰有一人命中率超過0.5的概率;
(3)在接下來的3場比賽中,用X表示這3場比賽中乙球員命中率超過0.5的場次,試寫出X的分布列,并求X的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}中,定義:dn=an+2+an﹣2an+1(n≥1),a1=1.
(1)若dn=an , a2=2,求an;
(2)若a2=﹣2,dn≥1,求證此數列滿足an≥﹣5(n∈N*);
(3)若|dn|=1,a2=1且數列{an}的周期為4,即an+4=an(n≥1),寫出所有符合條件的{dn}.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分別為AC,BC的中點,沿EF將△CEF折起,得到如圖2所示的四棱錐C′﹣ABFE
(1)求證:AB⊥平面AEC′;
(2)當四棱錐C′﹣ABFE體積取最大值時,
①若G為BC′中點,求異面直線GF與AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.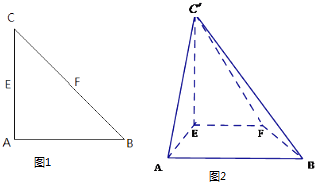
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】先閱讀下列結論的證法,再解決后面的問題:
已知 ![]() ,求證:
,求證: ![]() .
.
【證明】構造函數 ![]() ,則
,則 ![]() ,
,
因為對一切 ![]() ,恒有
,恒有 ![]() .
.
所以 ![]() ,從而得
,從而得 ![]() .
.
(1)若 ![]() ,請寫出上述結論的推廣式;
,請寫出上述結論的推廣式;
(2)參考上述解法,對你推廣的結論加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:x-2y+2m-2=0.
(1)求過點(2,3)且與直線l垂直的直線的方程;
(2)若直線l與兩坐標軸所圍成的三角形的面積大于4,求實數m的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)由直線![]() 的斜率為
的斜率為![]() ,可得所求直線的斜率為
,可得所求直線的斜率為![]() ,代入點斜式方程,可得答案;(2)直線
,代入點斜式方程,可得答案;(2)直線![]() 與兩坐標軸的交點分別為
與兩坐標軸的交點分別為![]() ,則所圍成的三角形的面積為
,則所圍成的三角形的面積為![]() ,根據直線
,根據直線![]() 與兩坐標軸所圍成的三角形的面積為大于
與兩坐標軸所圍成的三角形的面積為大于![]() ,構造不等式,解得答案.
,構造不等式,解得答案.
試題解析:(1)與直線l垂直的直線的斜率為-2,
因為點(2,3)在該直線上,所以所求直線方程為y-3=-2(x-2),
故所求的直線方程為2x+y-7=0.
(2) 直線l與兩坐標軸的交點分別為(-2m+2,0),(0,m-1),
則所圍成的三角形的面積為![]() ×|-2m+2|×|m-1|.
×|-2m+2|×|m-1|.
由題意可知![]() ×|-2m+2|×|m-1|>4,化簡得(m-1)2>4,
×|-2m+2|×|m-1|>4,化簡得(m-1)2>4,
解得m>3或m<-1,
所以實數m的取值范圍是(-∞,-1)∪(3,+∞).
【方法點睛】本題主要考查直線的方程,兩條直線平行與斜率的關系,屬于簡單題. 對直線位置關系的考查是熱點命題方向之一,這類問題以簡單題為主,主要考查兩直線垂直與兩直線平行兩種特殊關系:在斜率存在的前提下,(1)![]() ;(2)
;(2)![]() ,這類問題盡管簡單卻容易出錯,特別是容易遺忘斜率不存在的情況,這一點一定不能掉以輕心.
,這類問題盡管簡單卻容易出錯,特別是容易遺忘斜率不存在的情況,這一點一定不能掉以輕心.
【題型】解答題
【結束】
18
【題目】在平面直角坐標系![]() 中,已知經過原點O的直線
中,已知經過原點O的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點。
兩點。
(1)若直線![]() 與圓
與圓![]() 相切,切點為B,求直線
相切,切點為B,求直線![]() 的方程;
的方程;
(2)若![]() ,求直線
,求直線![]() 的方程;
的方程;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com