分析:(1)建立如圖所示空間直角坐標系,算出向量
、
的坐標,利用垂直向量數(shù)量積為0的方法建立方程組,算出平面D
1AC的一個法向量
=(2,1,2),結(jié)合平面DAC的一個法向量為
=(0,0,1)最后用空間向量的夾角公式即可算出二面角D
1-AC-D的余弦值;
(2)當λ=
時,可得E、F的坐標,從而
=(1,3,-2),進而算出
<,>的余弦值,再由
<,>為銳角,結(jié)合直線與平面所成角的定義,即可算出直線EF與平面D
1AC所成角的正弦值的大小;
(3)假設EF⊥EA,由
•=0建立關于λ的等式,化簡可得3λ
2-2λ+3=0,由根的判別式得該方程無解,所以原假設不成立,從而得到直線EF不可能與直線EA不可能垂直.
解答:解:(1)以DA、DC、DD
1為x、y、z軸,建立空間直角坐標系D-xyz,如圖所示.

則A(2,0,0),C(0,4,0),D
1(0,0,2),
=(2,0,-2),
=(0,4,-2). …(2分)
設平面D
1AC的法向量為
=(x,y,z),
則
•=0,•=0.
即x=z,z=2y.令y=1,則x=z=2.
∴平面D
1AC的一個法向量
=(2,1,2).…(4分)
又平面DAC的一個法向量為
=(0,0,1).
故
cos<,>===,
即二面角D
1-AC-D的余弦值為
. …(6分)
(2)當λ=
時,E(0,1,2),F(xiàn)(1,4,0),
=(1,3,-2).
所以
cos <,>===. …(9分)
因為
cos<,>>0,所以
<,>為銳角,
從而直線EF與平面D
1AC所成角的正弦值的大小為
. …(10分)
(3)假設EF⊥EA,則
•=0.
∵
E(0,,2),F(xiàn)(1,4,0),
∴
=(2,-,-2),
=(1,4-,-2). …(12分)
∴
2-(4-)+4=0.化簡得3λ
2-2λ+3=0.
該方程無解,所以假設不成立,即直線EF不可能與直線EA不可能垂直.…(14分)
點評:本題給出長方體模型,求二面角的余弦值和線面角的正弦值,并探索線線垂直的問題.著重考查了長方體的性質(zhì)、利用空間向量研究線面角與面面角等知識,屬于中檔題.

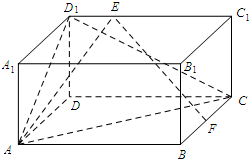 如圖,在長方體ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,點F是棱BC的中點,點E在棱C1D1上,且D1E=λEC1(λ為實數(shù)).
如圖,在長方體ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,點F是棱BC的中點,點E在棱C1D1上,且D1E=λEC1(λ為實數(shù)).


 閱讀快車系列答案
閱讀快車系列答案 如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內(nèi)接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側(cè)面積的最大值等于( )
如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內(nèi)接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側(cè)面積的最大值等于( )
![]() B.
B.![]() C.
C.![]() D.1
D.1
![]() B.
B.![]() C.
C.![]() D.1
D.1 .
. 
 ,AA1 =
,AA1 = ,M為側(cè)棱CC1上一點,AM⊥BA1.
,M為側(cè)棱CC1上一點,AM⊥BA1.