
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,設S為△ABC的面積,滿足S=![]() (a2+c2﹣b2).
(a2+c2﹣b2).
(1)求角B的大小;
(2)若邊b=![]() ,求a+c的取值范圍.
,求a+c的取值范圍.
【答案】(1)B=60°(2)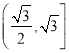
【解析】
(1)由三角形的面積公式,余弦定理化簡已知等式可求tanB的值,結合B的范圍可求B的值.
(2)由正弦定理,三角函數恒等變換的應用可求a+c![]() sin(A
sin(A![]() ),由題意可求范圍A
),由題意可求范圍A![]() ∈(
∈(![]() ,
,![]() ),根據正弦函數的圖象和性質即可求解.
),根據正弦函數的圖象和性質即可求解.
(1)在△ABC中,∵S![]() (a2+c2﹣b2)
(a2+c2﹣b2)![]() acsinB,cosB
acsinB,cosB![]() .
.
∴tanB![]() ,
,
∵B∈(0,π),
∴B![]() .
.
(2)∵B![]() ,b
,b![]() ,
,
∴由正弦定理可得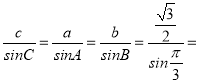 1,可得:a=sinA,c=sinC,
1,可得:a=sinA,c=sinC,
∴a+c=sinA+sinC=sinA+sin(![]() A)=sinA
A)=sinA![]() cosA
cosA![]() sinA
sinA![]() sin(A
sin(A![]() ),
),
∵A∈(0,![]() ),A
),A![]() ∈(
∈(![]() ,
,![]() ),
),
∴sin(A![]() )∈(
)∈(![]() ,1],
,1],
∴a+c![]() sin(A
sin(A![]() )∈(
)∈(![]() ,
,![]() ].
].


科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
,![]() 是平面α內的一組基向量,O為α內的定點,對于α內任意一點P,當
是平面α內的一組基向量,O為α內的定點,對于α內任意一點P,當![]() =x
=x![]() +y
+y![]() 時,則稱有序實數對(x,y)為點P的廣義坐標.若點A、B的廣義坐標分別為(x1,y1)(x2,y2),關于下列命題正確的是:()
時,則稱有序實數對(x,y)為點P的廣義坐標.若點A、B的廣義坐標分別為(x1,y1)(x2,y2),關于下列命題正確的是:()
A.線段A、B的中點的廣義坐標為(![]() );
);
B.A、B兩點間的距離為![]() ;
;
C.向量![]() 平行于向量
平行于向量![]() 的充要條件是x1y2=x2y1;
的充要條件是x1y2=x2y1;
D.向量![]() 垂直于
垂直于![]() 的充要條件是x1y2+x2y1=0
的充要條件是x1y2+x2y1=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】渦陽縣某華為手機專賣店對市民進行華為手機認可度的調查,在已購買華為手機的![]() 名市民中,隨機抽取
名市民中,隨機抽取![]() 名,按年齡(單位:歲)進行統計的頻數分布表和頻率分布直方圖如圖:
名,按年齡(單位:歲)進行統計的頻數分布表和頻率分布直方圖如圖:

分組(歲) | 頻數 |
|
|
|
|
|
|
|
|
|
|
合計 |
|
(1)求頻數分布表中![]() 、
、![]() 的值,并補全頻率分布直方圖;
的值,并補全頻率分布直方圖;
(2)在抽取的這![]() 名市民中,從年齡在
名市民中,從年齡在![]() 、
、![]() 內的市民中用分層抽樣的方法抽取
內的市民中用分層抽樣的方法抽取![]() 人參加華為手機宣傳活動,現從這
人參加華為手機宣傳活動,現從這![]() 人中隨機選取
人中隨機選取![]() 人各贈送一部華為手機,求這
人各贈送一部華為手機,求這![]() 人中恰有
人中恰有![]() 人的年齡在
人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}:1,﹣2,﹣2,3,3,3,﹣4,﹣4,﹣4,﹣4,…, ![]() ,…,即當
,…,即當 ![]() <n≤
<n≤ ![]() (k∈N*)時,
(k∈N*)時, ![]() .記Sn=a1+a2+…+an(n∈N).對于l∈N , 定義集合Pl=﹛n|Sn為an的整數倍,n∈N , 且1≤n≤l}
.記Sn=a1+a2+…+an(n∈N).對于l∈N , 定義集合Pl=﹛n|Sn為an的整數倍,n∈N , 且1≤n≤l}
(1)求P11中元素個數;
(2)求集合P2000中元素個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等腰直角三角形ABC中,AB=AC=4,點P是邊AB邊上異于AB的一點,光線從點P出發,經BC,CA反射后又回到點P(如圖),若光線QR經過△ABC的重心,則AP等于( )
A.2
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《厲害了,我的國》這部電影記錄:到2017年底,我國高鐵營運里程達2.5萬公里,位居世界第一位,超過第二名至第十名的總和,約占世界高鐵總量的三分之二.如圖是我國2009年至2017年高鐵營運里程(單位:萬公里)的折線圖.

根據這9年的高鐵營運里程,甲、乙兩位同學分別選擇了![]() 與時間變量
與時間變量![]() 的兩個回歸模型①:
的兩個回歸模型①:![]() ;②
;②![]() .
.
(1)求![]() ,
,![]() (精確到0.01);
(精確到0.01);
(2)乙求得模型②的回歸方程為![]() ,你認為哪個模型的擬合效果更好?并說明理由.
,你認為哪個模型的擬合效果更好?并說明理由.
附:參考公式: ,
,![]() ,
,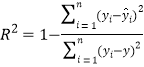 .
.
參考數據:
|
|
|
|
|
|
1.39 | 76.94 | 285 | 0.22 | 0.09 | 3.72 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解當下高二男生的身高狀況,某地區對高二年級男生的身高(單位: ![]() )進行了抽樣調查,得到的頻率分布直方圖如圖所示.已知身高在
)進行了抽樣調查,得到的頻率分布直方圖如圖所示.已知身高在![]() 之間的男生人數比身高在
之間的男生人數比身高在![]() 之間的人數少1人.
之間的人數少1人.
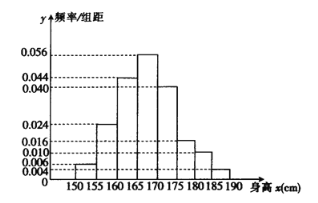
(1)若身高在![]() 以內的定義為身高正常,而該地區共有高二男生18000人,則該地區高二男生中身高正常的大約有多少人?
以內的定義為身高正常,而該地區共有高二男生18000人,則該地區高二男生中身高正常的大約有多少人?
(2)從所抽取的樣本中身高在![]() 和
和![]() 的男生中隨機再選出2人調查其平時體育鍛煉習慣對身高的影響,則所選出的2人中至少有一人身高大于185
的男生中隨機再選出2人調查其平時體育鍛煉習慣對身高的影響,則所選出的2人中至少有一人身高大于185![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個幾何體的三視圖如圖所示,該幾何體從上到下由四個簡單幾何體組成,其體積分別記為V1 , V2 , V3 , V4 , 上面兩個簡單幾何體均為旋轉體,下面兩個簡單幾何體均為多面體,則有( ) 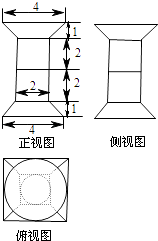
A.V1<V2<V4<V3
B.V1<V3<V2<V4
C.V2<V1<V3<V4
D.V2<V3<V1<V4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分別是AC,AB上的點, ![]() ,O為BC的中點.將△ADE沿DE折起,得到如圖2所示的四棱椎A′﹣BCDE,其中A′O=
,O為BC的中點.將△ADE沿DE折起,得到如圖2所示的四棱椎A′﹣BCDE,其中A′O= ![]() .
. 
(1)證明:A′O⊥平面BCDE;
(2)求二面角A′﹣CD﹣B的平面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com