【題目】已知兩個定點
，動點
滿足
.設動點的軌跡為曲線
，直線
.
（1）求曲線的軌跡方程；
（2）若
與曲線交于不同的
兩點，且
（
為坐標原點），求直線的斜率；
（3）若
， 
是直線上的動點，過作曲線的兩條切線
，切點為
，探究：直線
是否過定點.
【答案】（1）
；（2）
；（3）
.
【解析】
（1）設點P坐標為（x，y），運用兩點的距離公式，化簡整理，即可得到所求軌跡的方程；（2）由
，則點
到
邊的距離為
，由點到線的距離公式得直線
的斜率；（3）由題意可知：O，Q，M，N四點共圓且在以OQ為直徑的圓上，設
，則圓
的圓心為
運用直徑式圓的方程，得直線
的方程為
，結合直線系方程，即可得到所求定點．
（1）設點
的坐標為
由
可得，
，
整理可得
所以曲線
的軌跡方程為.
（2）依題意，
，且，則點到邊的距離為
即點
到直線
的距離
，解得
所以直線的斜率為.
（3）依題意，
，則
都在以
為直徑的圓上
是直線
上的動點，設
則圓的圓心為，且經過坐標原點
即圓的方程為
，
又因為
在曲線
上
由
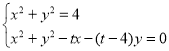，可得
即直線的方程為
由
且
可得，
解得
所以直線是過定點.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】如圖，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四邊形ACFE為矩形，平面ACFE⊥平面ABCD，CF=1．
（Ⅰ）求證：BC⊥平面ACFE；
（Ⅱ）點M在線段EF上運動，設平面MAB與平面FCB所成二面角的平面角為θ（θ≤90°），試求cosθ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程為
（
為參數），在以原點為極點， 
軸正半軸為極軸的極坐標系中，直線
的極坐標方程為
．
（1）求曲線
的普通方程和直線
的傾斜角；
（2）設點
，直線
和曲線
交于
兩點，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種產品的廣告費支出x與銷售額y(單位：萬元)之間有如下對應數據：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）若廣告費與銷售額具有相關關系，求回歸直線方程；
（2）在已有的五組數據中任意抽取兩組，求兩組數據其預測值與實際值之差的絕對值都不超過5的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，已知
，
，動點
滿足
，設動點
的軌跡為曲線
．
（1）求動點的軌跡方程，并說明曲線是什么圖形；
（2）過點
的直線
與曲線交于
兩點，若
，求直線的方程；
（3）設
是直線
上的點，過點作曲線的切線
，切點為
，設
，求證：過
三點的圓必過定點，并求出所有定點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】校運動會高二理三個班級的3名同學報名參加鉛球、跳高、三級跳遠3個運動項目，每名同學都可以從3個運動項目中隨機選擇一個,且每個人的選擇相互獨立.
(1)求3名同學恰好選擇了2個不同運動項目的概率；
(Ⅱ)設選擇跳高的人數為
試求的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
