
【題目】已知橢圓![]() ,點P(2,0).
,點P(2,0).
(I)求橢圓C的短軸長與離心率;
( II)過(1,0)的直線![]() 與橢圓C相交于M、N兩點,設(shè)MN的中點為T,判斷|TP|與|TM|的大小,并證明你的結(jié)論.
與橢圓C相交于M、N兩點,設(shè)MN的中點為T,判斷|TP|與|TM|的大小,并證明你的結(jié)論.
【答案】(Ⅰ)短軸長為![]() ,離心率為
,離心率為![]() .(Ⅱ)見解析
.(Ⅱ)見解析
【解析】分析:(Ⅰ)由題意可得![]() ,
,![]() ,于是可得短軸長與離心率.(Ⅱ)方法一:通過判斷點P與以MN為直徑的圓的位置關(guān)系可得結(jié)論.方法二:運用作差比較的方法判斷大小關(guān)系.
,于是可得短軸長與離心率.(Ⅱ)方法一:通過判斷點P與以MN為直徑的圓的位置關(guān)系可得結(jié)論.方法二:運用作差比較的方法判斷大小關(guān)系.
詳解:(I)由題意的橢圓的方程為![]() ,
,
∴![]()
∴![]() ,
,![]() .
.
∴橢圓C的短軸長為![]() ,離心率為
,離心率為![]() .
.
(II)方法1:結(jié)論是:![]() .
.
當直線![]() 斜率不存在時,
斜率不存在時,![]() .
.
當直線![]() 斜率存在時,設(shè)直線
斜率存在時,設(shè)直線![]()
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直線![]() 與橢圓交于兩點,
與橢圓交于兩點,
∴![]() .
.
設(shè)![]() ,
,
則![]() .
.
又![]()
![]()
![]()
![]()
![]()
∴![]() ,
,
∴點P在以MN為直徑的圓內(nèi),
故![]() .
.
(II)方法2:結(jié)論是![]() .
.
當直線![]() 斜率不存在時,
斜率不存在時,![]()
當直線![]() 斜率存在時,設(shè)直線
斜率存在時,設(shè)直線![]()
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直線![]() 與橢圓交于兩點,
與橢圓交于兩點,
∴![]() .
.
設(shè)![]() ,
,
則![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]()
![]() ,
,
∵![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=ex+![]() .
.
(I)當a=![]() 時,求函數(shù)f(x)在x=0處的切線方程;
時,求函數(shù)f(x)在x=0處的切線方程;
(II)函數(shù)f(x)是否存在零點?若存在,求出零點的個數(shù);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某廠為檢驗車間一生產(chǎn)線是否工作正常,現(xiàn)從生產(chǎn)線中隨機抽取一批零件樣本,測量尺寸(單位: mm )繪成頻率分布直方圖如圖所示:
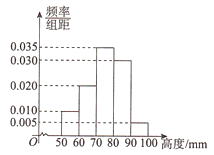
(Ⅰ)求該批零件樣本尺寸的平均數(shù) x 和樣本方差 ![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(Ⅱ)若該批零件尺寸![]() 服從正態(tài)分布
服從正態(tài)分布 ![]() ,其中
,其中 ![]() 近似為樣本平均數(shù)
近似為樣本平均數(shù) ![]() 近似為樣本方差
近似為樣本方差 ![]() ,利用該正態(tài)分布求
,利用該正態(tài)分布求 ![]() ;
;
(Ⅲ)若從生產(chǎn)線中任取一零件,測量尺寸為30mm,根據(jù) ![]() 原則判斷該生產(chǎn)線是否正常?
原則判斷該生產(chǎn)線是否正常?
附: ![]() ;若
;若![]() ,則
,則 ![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】用a代表紅球,b代表藍球,c代表黑球,由加法原理及乘法原理,從1個紅球和1個藍球中取出若干個球的所有取法可由(1+a)(1+b)的展開式1+a+b+ab表示出來,如:“1”表示一個球都不取、“a”表示取出一個紅球,而“ab”則表示把紅球和藍球都取出來.以此類推,下列各式中,其展開式可用來表示從5個無區(qū)別的紅球、5個無區(qū)別的藍球、5個有區(qū)別的黑球中取出若干個球,且所有的藍球都取出或都不取出的所有取法的是( )
A.(1+a+a2+a3+a4+a5)(1+b5)(1+c)5
B.(1+a5)(1+b+b2+b3+b4+b5)(1+c)5
C.(1+a)5(1+b+b2+b3+b4+b5)(1+c5)
D.(1+a5)(1+b)5(1+c+c2+c3+c4+c5)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)F為拋物線![]() 的焦點,A、B是拋物線C上的兩個動點,O為坐標原點.
的焦點,A、B是拋物線C上的兩個動點,O為坐標原點.
(I)若直線AB經(jīng)過焦點F,且斜率為2,求線段AB的長度|AB|;
(II)當OA⊥OB時,求證:直線AB經(jīng)過定點M(4,0).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)![]() ,
, ![]() ,已知
,已知![]() 和
和![]() 在
在![]() 處有相同的切線.
處有相同的切線.
(1)求![]() ,
, ![]() 的解析式;
的解析式;
(2)求![]() 在
在![]() 上的最小值;
上的最小值;
(3)若對![]() ,
, ![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
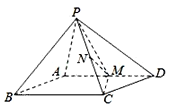
【題目】如圖,已知四棱錐P-ABCD的底面ABCD是平行四邊形,PA⊥平面ABCD.M是AD的中點,N是PC的中點.
(1)求證:MN∥平面PAB;
(2)若平面PMC⊥平面PAD,求證:CM⊥AD;
(3)若平面ABCD是矩形,PA=AB,求證:平面PMC⊥平面PBC.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)△ABC的三個內(nèi)角A,B,C所對的邊分別為a,b,c.已知sin![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=2,求b+c的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com