
【題目】以雙曲線![]() 上一點
上一點![]() 為圓心作圓,該圓與
為圓心作圓,該圓與![]() 軸相切于
軸相切于![]() 的一個焦點
的一個焦點![]() ,與
,與![]() 軸交于
軸交于![]() 兩點,若
兩點,若![]() ,則雙曲線
,則雙曲線![]() 的離心率________.
的離心率________.
【答案】![]()
【解析】
由題意可設(shè)F(c,0),MF⊥x軸,可設(shè)M(c,n),n>0,設(shè)x=c,代入雙曲線的方程,可得M的坐標(biāo),圓的半徑,運用弦長公式,可得|PQ|=2![]() c,可得a,c的方程,運用離心率公式計算即可得到所求值.
c,可得a,c的方程,運用離心率公式計算即可得到所求值.
由題意可設(shè)F(c,0),
MF⊥x軸,可設(shè)M(c,n),n>0,
設(shè)x=c,代入雙曲線的方程可得y=b![]() ,
,
即有M(c,![]() ),
),
可得圓的圓心為M,半徑為![]() ,
,
即有M到y軸的距離為c,
可得|PQ|=2![]() c,
c,
化簡可得3b4=4a2c2,
由c2=a2+b2,可得3c4﹣10c2a2+3a4=0,
由e![]() ,可得3e4﹣10e2+3=0,
,可得3e4﹣10e2+3=0,
解得e2=3(![]() 舍去),
舍去),
即有e![]() .
.
故答案為:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
⑴求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
⑵如果對于任意的![]() ,
,![]() 總成立,求實數(shù)
總成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合![]() ,若對于任意實數(shù)對
,若對于任意實數(shù)對![]() ,存在
,存在![]() ,使
,使![]() 成立,則稱集合
成立,則稱集合![]() 是“垂直對點集” .給出下列四個集合:
是“垂直對點集” .給出下列四個集合:
① ![]() ;
;
②![]() ;
;
③ ![]() ;
;
④![]() .
.
其中是“垂直對點集”的序號是( ).
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,將曲線
中,將曲線![]() (
(![]() 為參數(shù))上任意一點
為參數(shù))上任意一點![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換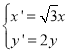 后得到曲線
后得到曲線![]() 的圖形.以坐標(biāo)原點
的圖形.以坐標(biāo)原點![]() 為極點,x軸的非負(fù)半軸為極軸,取相同的單位長度建立極坐標(biāo)系,已知直線
為極點,x軸的非負(fù)半軸為極軸,取相同的單位長度建立極坐標(biāo)系,已知直線![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)點P為曲線![]() 上的任意一點,求點P到直線
上的任意一點,求點P到直線![]() 的距離的最大值及取得最大值時點P的坐標(biāo).
的距離的最大值及取得最大值時點P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,將曲線
中,將曲線![]() (
(![]() 為參數(shù))上任意一點
為參數(shù))上任意一點![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換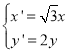 后得到曲線
后得到曲線![]() 的圖形.以坐標(biāo)原點
的圖形.以坐標(biāo)原點![]() 為極點,x軸的非負(fù)半軸為極軸,取相同的單位長度建立極坐標(biāo)系,已知直線
為極點,x軸的非負(fù)半軸為極軸,取相同的單位長度建立極坐標(biāo)系,已知直線![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)點P為曲線![]() 上的任意一點,求點P到直線
上的任意一點,求點P到直線![]() 的距離的最大值及取得最大值時點P的坐標(biāo).
的距離的最大值及取得最大值時點P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某大學(xué)進(jìn)行自主招生測試,需要對邏輯思維和閱讀表達(dá)進(jìn)行能力測試.學(xué)校對參加測試的200名學(xué)生的邏輯思維成績、閱讀表達(dá)成績以及這兩項的總成績進(jìn)行了排名.其中甲、乙、丙三位同學(xué)的排名情況如圖所示,下列敘述正確的是( )
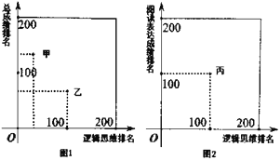
A.甲同學(xué)的邏輯思維成績排名比他的閱讀表達(dá)成績排名更靠前
B.乙同學(xué)的邏輯思維成績排名比他的閱讀表達(dá)成績排名更靠前
C.甲、乙、丙三位同學(xué)的邏輯思維成績排名中,甲同學(xué)更靠前
D.甲同學(xué)的總成績排名比丙同學(xué)的總成績排名更靠前
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司進(jìn)行共享單車的投放與損耗統(tǒng)計,到去年![]() 年底單車的市場保有量(已投入市場且能正常使用的單車數(shù)量)為
年底單車的市場保有量(已投入市場且能正常使用的單車數(shù)量)為![]() 輛,預(yù)計今后每年新增單車1000輛,隨著單車的頻繁使用,估計每年將有200輛車的損耗,并且今后若干年內(nèi),年平均損耗在上一年損耗基礎(chǔ)上增加
輛,預(yù)計今后每年新增單車1000輛,隨著單車的頻繁使用,估計每年將有200輛車的損耗,并且今后若干年內(nèi),年平均損耗在上一年損耗基礎(chǔ)上增加![]() %.
%.
(1)預(yù)計![]() 年底單車的市場保有量是多少?
年底單車的市場保有量是多少?
(2)到哪一年底,市場的單車保有量達(dá)到最多?該年的單車保有量是多少輛(最后結(jié)果精確到整數(shù))?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com