把命題“若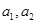
是正實(shí)數(shù)，則有
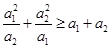”推廣到一般情形，推廣后的命題為_(kāi)___________.
若
都是正數(shù)，則有
解析試題分析：可通過(guò)類(lèi)比，歸納得一般結(jié)論，證明如下：
考點(diǎn)：推理與證明.
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題
用反證法證明命題：“已知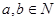
,若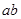
可被5整除，則
中至少有一個(gè)能被5整除”時(shí)，反設(shè)正確的是( )
| A．都不能被5整除 | B．都能被5整除 |
| C．中有一個(gè)不能被5整除 | D．中有一個(gè)能被5整除 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題
下列說(shuō)法正確的個(gè)數(shù)是 ( )
①演繹推理是由一般到特殊的推理
②演繹推理得到的結(jié)論一定是正確的
③演繹推理的一般模式是“三段論”形式
④演繹推理得到的結(jié)論的正誤與大前提、小前提和推理形式有關(guān)
| A．1 | B．2 | C．3 | D．4 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題
下列推理是歸納推理的是
| A．A，B為定點(diǎn)，動(dòng)點(diǎn)P滿(mǎn)足|PA|＋|PB|＝2a＞|AB|，則P點(diǎn)的軌跡為橢圓 |
| B．由a1＝1，an＝3n－1，求出S1，S2，S3，猜想出數(shù)列的前n項(xiàng)和Sn的表達(dá)式 |
C．由圓x2＋y2＝r2的面積πr2，猜想出橢圓 ＋ ＝1的面積S＝πab |
| D．科學(xué)家利用魚(yú)的沉浮原理制造潛艇 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題
古希臘畢達(dá)哥拉斯學(xué)派的數(shù)學(xué)家研究過(guò)各種多邊形數(shù)。如三角形數(shù)1,3,6,10···，第n個(gè)三角形數(shù)為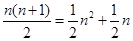
。記第n個(gè)k邊形數(shù)為N(n,k)(
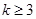),以下列出了部分k邊形數(shù)中第n個(gè)數(shù)的表達(dá)式：
三角形數(shù) N(n,3)=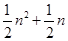
正方形數(shù) N(n,4)=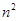
五邊形數(shù) N(n,5)=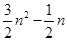
六邊形數(shù) N(n,6)=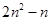
可以推測(cè)N(n,k)的表達(dá)式，由此計(jì)算N(10,24)= ____________
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題
用數(shù)學(xué)歸納法證明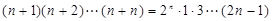
（
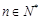）時(shí)，從“n=
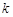”到“n=
”的證明，左邊需增添的代數(shù)式是___________.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題
完成反證法證題的全過(guò)程．設(shè)a1,a2, ,a7是1,2, ,7的一個(gè)排列,求證:乘積p=(a1-1)(a2-2) (a7-7)為偶數(shù)．
證明:假設(shè)p為奇數(shù),則a1-1,a2-2, ,a7-7均為奇數(shù)．因奇數(shù)個(gè)奇數(shù)之和為奇數(shù),故有奇數(shù)= = =0．但0≠奇數(shù),這一矛盾說(shuō)明p為偶數(shù)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題
有一段演繹推理是這樣的:“若直線(xiàn)平行于平面,則該直線(xiàn)平行于平面內(nèi)所有直線(xiàn);已知直線(xiàn)b∥平面α,直線(xiàn)a?平面α,則直線(xiàn)b∥直線(xiàn)a”,結(jié)論顯然是錯(cuò)誤的,這是因?yàn)? )
| A．大前提錯(cuò)誤 | B．小前提錯(cuò)誤 |
| C．推理形式錯(cuò)誤 | D．非以上錯(cuò)誤 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà)：027-86699610 舉報(bào)郵箱：58377363@163.com
則
______;