
【題目】如圖,矩形![]() 是一個歷史文物展覽廳的俯視圖,點
是一個歷史文物展覽廳的俯視圖,點![]() 在
在![]() 上,在梯形
上,在梯形![]() 區域內部展示文物,
區域內部展示文物,![]() 是玻璃幕墻,游客只能在
是玻璃幕墻,游客只能在![]() 區域內參觀.在
區域內參觀.在![]() 上點
上點![]() 處安裝一可旋轉的監控攝像頭.
處安裝一可旋轉的監控攝像頭.![]() 為監控角,其中
為監控角,其中![]() 、
、![]() 在線段
在線段![]() (含端點)上,且點
(含端點)上,且點![]() 在點
在點![]() 的右下方.經測量得知:
的右下方.經測量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .記
.記![]() (弧度),監控攝像頭的可視區域
(弧度),監控攝像頭的可視區域![]() 的面積為
的面積為![]() 平方米.
平方米.

(1)求![]() 關于
關于![]() 的函數關系式,并寫出
的函數關系式,并寫出![]() 的取值范圍;(參考數據:
的取值范圍;(參考數據:![]() )
)
(2)求![]() 的最小值.
的最小值.
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:噸)和年利潤
(單位:噸)和年利潤![]() (單位:萬元)的影響.對近六年的年宣傳費
(單位:萬元)的影響.對近六年的年宣傳費![]() 和年銷售量
和年銷售量![]() 的數據作了初步統計,得到如下數據:
的數據作了初步統計,得到如下數據:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣傳費 | 38 | 48 | 58 | 68 | 78 | 88 |
年銷售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
經電腦模擬,發現年宣傳費![]() (萬元)與年銷售量
(萬元)與年銷售量![]() (噸)之間近似滿足關系式
(噸)之間近似滿足關系式![]() ,即
,即![]() .對上述數據作了初步處理,得到相關的值如下表:
.對上述數據作了初步處理,得到相關的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根據所給數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)規定當產品的年銷售量![]() (噸)與年宣傳費
(噸)與年宣傳費![]() (萬元)的比值在區間
(萬元)的比值在區間![]() 內時認為該年效益良好.該公司某
內時認為該年效益良好.該公司某![]() 年投入的宣傳費用(單位:萬元)分別為:
年投入的宣傳費用(單位:萬元)分別為:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,試根據回歸方程估計年銷售量,從這
,試根據回歸方程估計年銷售量,從這![]() 年中任選
年中任選![]() 年,記其中選到效益良好年的數量為
年,記其中選到效益良好年的數量為![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 為自然對數的底數,
為自然對數的底數,![]() )
)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國某沙漠,曾被稱為“死亡之海”,截止2018年年底該地區的綠化率只有![]() ,計劃從2019年開始使用無人機飛播造林,彈射的種子可以直接打入沙面里頭,實現快速播種,每年原來沙漠面積的
,計劃從2019年開始使用無人機飛播造林,彈射的種子可以直接打入沙面里頭,實現快速播種,每年原來沙漠面積的![]() 將被改為綠洲,但同時原有綠洲面積的
將被改為綠洲,但同時原有綠洲面積的![]() 還會被沙漠化。設該地區的面積為
還會被沙漠化。設該地區的面積為![]() ,2018年年底綠洲面積為
,2018年年底綠洲面積為![]() ,經過一年綠洲面積為
,經過一年綠洲面積為![]() ……經過
……經過![]() 年綠洲面積為
年綠洲面積為![]() ,
,
(1)求經過![]() 年綠洲面積
年綠洲面積![]() ;
;
(2)截止到哪一年年底,才能使該地區綠洲面積超過![]() ?(取
?(取![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分別為AC、DC的中點. 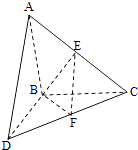
(1)求證:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某濕地公園內有一條河,現打算建一座橋將河兩岸的路連接起來,剖面設計圖紙如下:

其中,點![]() 為
為![]() 軸上關于原點對稱的兩點,曲線段
軸上關于原點對稱的兩點,曲線段![]() 是橋的主體,
是橋的主體,![]() 為橋頂,且曲線段
為橋頂,且曲線段![]() 在圖紙上的圖形對應函數的解析式為
在圖紙上的圖形對應函數的解析式為![]() ,曲線段
,曲線段![]() 均為開口向上的拋物線段,且
均為開口向上的拋物線段,且![]() 分別為兩拋物線的頂點,設計時要求:保持兩曲線在各銜接處(
分別為兩拋物線的頂點,設計時要求:保持兩曲線在各銜接處(![]() )的切線的斜率相等.
)的切線的斜率相等.
(1)求曲線段![]() 在圖紙上對應函數的解析式,并寫出定義域;
在圖紙上對應函數的解析式,并寫出定義域;
(2)車輛從![]() 經
經![]() 倒
倒![]() 爬坡,定義車輛上橋過程中某點
爬坡,定義車輛上橋過程中某點![]() 所需要的爬坡能力為:
所需要的爬坡能力為:![]() (該點
(該點![]() 與橋頂間的水平距離)
與橋頂間的水平距離)![]() (設計圖紙上該點處的切線的斜率),其中
(設計圖紙上該點處的切線的斜率),其中![]() 的單位:米.若該景區可提供三種類型的觀光車:①游客踏乘;②蓄電池動力;③內燃機動力.它們的爬坡能力分別為
的單位:米.若該景區可提供三種類型的觀光車:①游客踏乘;②蓄電池動力;③內燃機動力.它們的爬坡能力分別為![]() 米,
米,![]() 米,
米,![]() 米,又已知圖紙上一個單位長度表示實際長度
米,又已知圖紙上一個單位長度表示實際長度![]() 米,試問三種類型的觀光車是否都可以順利過橋?
米,試問三種類型的觀光車是否都可以順利過橋?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的一段圖象過點
的一段圖象過點![]() ,如圖所示.
,如圖所示.
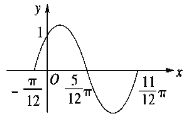
(1)求函數![]() 的表達式;
的表達式;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位,得函數
個單位,得函數![]() 的圖象,求
的圖象,求![]() 的最大值,并求出此時自變量
的最大值,并求出此時自變量![]() 的集合,并寫出該函數的增區間.
的集合,并寫出該函數的增區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com