【題目】在平面內，定點A、B、C、D滿足：| 
|=| 
|=| 
|， = 
= =﹣2，動點P、M滿足：| 
|=1， 
= 
，則| 
|的最大值是 ．
【答案】
【解析】解：∵| 
|=| 
|=| 
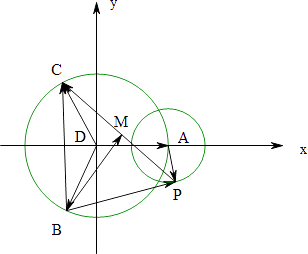
|，∴A，B，C在以D為圓心的圓D上，
∵ = 
= =﹣2，∴ 
兩兩夾角相等均為120°，∴|DA|=2，
以D為原點建立平面直角坐標系，設A（2，0），則B（﹣1，﹣ 
），C（﹣1， ），
∴ 
=（0，2 ）．
∵| 
|=1，∴P在以A為圓心，以1為半徑的圓A上，
∵ 
= 
，∴M為PC的中點，∴ 
= 
（ 
）．
設P（2+cosα，sinα），則 
=（3+cosα，sinα+ ），
∴ =（ cosα+ 
， sinα+ 
），
∴ 
=（ cosα+ ）2+（ sinα+ ）2= 
+ sinα+ 
=3sin（α+ 
）+ ，
∴| |的最大值為 
= ．
所以答案是： ．
輕松暑假總復習系列答案科目：高中數學 來源： 題型：
【題目】求適合下列條件的圓錐曲線的標準方程：
（1）焦點坐標為（ 
，0），準線方程為x= 
的橢圓；
（2）過點（ ，2），漸近線方程為y=±2x的雙曲線．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2017福建三明5月質檢】某市政府為了引導居民合理用水，決定全面實施階梯水價，階梯水價原則上以住宅（一套住宅為一戶）的月用水量為基準定價：若用水量不超過12噸時，按4元/噸計算水費；若用水量超過12噸且不超過14噸時，超過12噸部分按6.60元/噸計算水費；若用水量超過14噸時，超過14噸部分按7.80元/噸計算水費．為了了解全市居民月用水量的分布情況，通過抽樣，獲得了100戶居民的月用水量（單位：噸），將數據按照
分成8組，制成了如圖1所示的頻率分布直方圖．
（Ⅰ）假設用抽到的100戶居民月用水量作為樣本估計全市的居民用水情況．
（ⅰ）現從全市居民中依次隨機抽取5戶，求這5戶居民恰好3戶居民的月用水用量都超過12噸的概率；
（ⅱ）試估計全市居民用水價格的期望（精確到0.01）；
（Ⅱ）如圖2是該市居民李某2016年1～6月份的月用水費
（元）與月份
的散點圖，其擬合的線性回歸方程是
．若李某2016年1～7月份水費總支出為294.6元，試估計李某7月份的用水噸數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓O：x2+y2=1和定點A（2，1），由圓O外一點P（a，b）向圓O引切線PQ，PM，切點為Q，M，且滿足|PQ|=|PA|． 
（1）求實數a，b間滿足的等量關系；
（2）若以P為圓心的圓P與圓O有公共點，試求圓P的半徑最小時圓P的方程；
（3）當P點的位置發生變化時，直線QM是否過定點，如果是，求出定點坐標，如果不是，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正項數列{an}的前n項和Sn滿足：Sn2﹣（n2+n﹣1）Sn﹣（n2+n）=0
（1）求數列{an}的通項公式an；
（2）令bn= 
，求數列{bn}的前n項和Tn ， 證明：對于任意的n∈N* ， 都有Tn 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，AB=1，AC=AA1=
， ∠ABC=60°．
（1）證明：AB⊥A1C；
（2）求二面角A﹣A1C﹣B的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若某校高一年級8個班參加合唱比賽的得分如莖葉圖所示，則這組數據的中位數和平均數分別是（ ） 
A.91.5和91.5
B.91.5和92
C.91和91.5
D.92和92
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】福州市某大型家電商場為了使每月銷售空調和冰箱獲得的總利潤達到最大，對某月即將出售的空調和冰箱進行了相關調查，得出下表：
資金 | 每臺空調或冰箱所需資金（百元） | 月資金最多供應量（百元） | |
空調 | 冰箱 | ||
進貨成本 | 30 | 20 | 300 |
工人工資 | 5 | 10 | 110 |
每臺利潤 | 6 | 8 | |
問：該商場如果根據調查得來的數據，應該怎樣確定空調和冰箱的月供應量，才能使商場獲得的總利潤最大？總利潤的最大值為多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
