
已知數(shù)列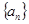 的前
的前 項和
項和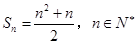 .
.
(1)求數(shù)列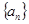 的通項公式;
的通項公式;
(2)設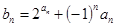 ,求數(shù)列
,求數(shù)列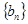 的前
的前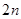 項和.
項和.
(1)  (2)
(2) 
解析試題分析:(1)題目已知 之間的關(guān)系,令
之間的關(guān)系,令 ,利用
,利用 ,即可求的
,即可求的 的值,令
的值,令 ,利用
,利用 與前n項和之間的關(guān)系
與前n項和之間的關(guān)系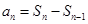 即可得到
即可得到 ,令
,令 檢驗首項即可得到
檢驗首項即可得到 的通項公式.
的通項公式.
(2)把(1)得到的通項公式代入 可以得到
可以得到 是由等比數(shù)列
是由等比數(shù)列 ,數(shù)列
,數(shù)列 之和,才用分組求和法,首先利用等比數(shù)列前n項和公式求的等比數(shù)列
之和,才用分組求和法,首先利用等比數(shù)列前n項和公式求的等比數(shù)列 的前n項和,再利用
的前n項和,再利用 對數(shù)列
對數(shù)列 進行分組
進行分組 即可求的數(shù)列
即可求的數(shù)列 的前n項和
的前n項和
(1)當 時,
時, ;
;
當 時,
時,
檢驗首項 符合
符合 ,所以數(shù)列
,所以數(shù)列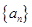 的通項公式為
的通項公式為 .
.
(2)由(1)可得 ,記數(shù)列
,記數(shù)列 的前
的前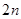 項和為
項和為 ,
,
則


故數(shù)列 的前
的前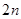 項和為
項和為
考點:數(shù)列前 項和 等差數(shù)列 等比數(shù)列 分組求和法
項和 等差數(shù)列 等比數(shù)列 分組求和法


科目:高中數(shù)學 來源: 題型:解答題
在等比數(shù)列{an}中,an>0(n∈N*),且a1a3=4,a3+1是a2和a4的等差中項.
(1)求數(shù)列{an}的通項公式;
(2)若數(shù)列{bn}滿足bn=an+1+log2an(n=1,2,3,…),求數(shù)列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
數(shù)列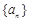 滿足
滿足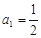 ,
,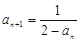
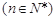 .
.
(1)求證: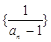 為等差數(shù)列,并求出
為等差數(shù)列,并求出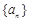 的通項公式;
的通項公式;
(2)設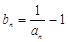 ,數(shù)列
,數(shù)列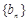 的前
的前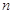 項和為
項和為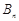 ,對任意
,對任意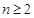 都有
都有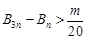 成立,求整數(shù)
成立,求整數(shù)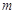 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(滿分16分)
設數(shù)列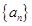 的前
的前 項和為
項和為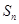 .若對任意的正整數(shù)
.若對任意的正整數(shù) ,總存在正整數(shù)
,總存在正整數(shù) ,使得
,使得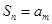 ,則稱
,則稱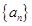 是“
是“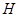 數(shù)列”.
數(shù)列”.
(1)若數(shù)列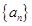 的前
的前 項和為
項和為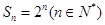 ,證明:
,證明: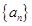 是“
是“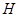 數(shù)列”.
數(shù)列”.
(2)設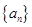 是等差數(shù)列,其首項
是等差數(shù)列,其首項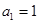 ,公差
,公差 ,若
,若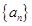 是“
是“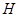 數(shù)列”,求
數(shù)列”,求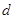 的值;
的值;
(3)證明:對任意的等差數(shù)列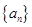 ,總存在兩個“
,總存在兩個“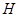 數(shù)列”
數(shù)列” 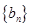 和
和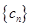 ,使得
,使得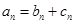
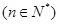 成立.
成立.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本題滿分18分)本題共3個小題,第1小題滿分3分,第2小題滿分6分,第3小題滿分9分.
已知數(shù)列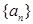 滿足
滿足 .
.
若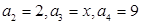 ,求
,求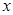 的取值范圍;
的取值范圍;
若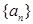 是公比為
是公比為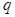 等比數(shù)列,
等比數(shù)列,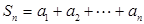 ,
,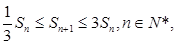 求
求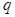 的取值范圍;
的取值范圍;
若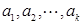 成等差數(shù)列,且
成等差數(shù)列,且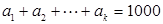 ,求正整數(shù)
,求正整數(shù)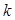 的最大值,以及
的最大值,以及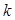 取最大值時相應數(shù)列
取最大值時相應數(shù)列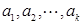 的公差.
的公差.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知數(shù)列{an}是公差不為0的等差數(shù)列,a1=2,且a2,a3,a4+1成等比數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)設bn=an+2an,求數(shù)列{bn}的前n項和Sn.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com