
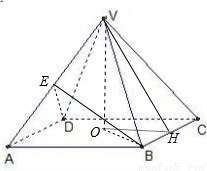
 如圖,正四棱錐S-ABCD,設AB=2,高VO=h.H為BC中點.
如圖,正四棱錐S-ABCD,設AB=2,高VO=h.H為BC中點.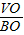 =
=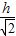 ,
, =h,
=h,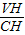 =
= ,
,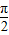 .
. VA×BE=
VA×BE= ×BC×VH,即
×BC×VH,即
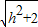 ×BE=
×BE= ×2×
×2×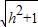 ,BE2=
,BE2=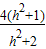 ,DE2+BE2=2DE2<BD2,∴∠BED為鈍角,
,DE2+BE2=2DE2<BD2,∴∠BED為鈍角,

科目:高中數學 來源: 題型:
 如圖,正四棱錐S-ABCD中,E是側棱SC的中點,異面直線SA和BC所成角的大小是60°.
如圖,正四棱錐S-ABCD中,E是側棱SC的中點,異面直線SA和BC所成角的大小是60°.查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
 12、如圖在正四棱錐S-ABCD中,E是BC的中點,P點在側面△SCD內及其邊界上運動,并且總是保持PE⊥AC,則動點P的軌跡與△SCD組成的相關圖形是( )
12、如圖在正四棱錐S-ABCD中,E是BC的中點,P點在側面△SCD內及其邊界上運動,并且總是保持PE⊥AC,則動點P的軌跡與△SCD組成的相關圖形是( )查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com