
(1)求證:AM∥平面BDE;
(2)求證:AM⊥平面BDF;
(3)求二面角ADFB的大小.
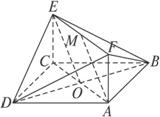
解法一:(1)證明:記AC與BD的交點為O,連結OE,

∵O、M分別是AC、EF的中點,四邊形ACEF是矩形,
∴四邊形AOEM是平行四邊形.
∴AM∥OE.
∵OE![]() 平面BDE,AM
平面BDE,AM![]() 平面BDE,
平面BDE,
∴AM∥平面BDE.
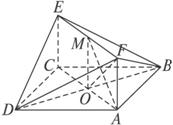
(2)證明:∵BD⊥AC,BD⊥AF,且AC交AF于A,
∴BD⊥平面AE.
又∵AM![]() 平面AE,
平面AE,
∴BD⊥AM.
∵AD=![]() ,AF=1,OA=1,
,AF=1,OA=1,
∴AOMF是正方形.
∴AM⊥OF.又AM⊥BD,且OF∩BD=O,
∴AM⊥平面BDF.
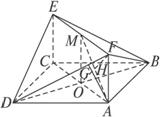
(3)解:設AM∩OF=H,過H作HG⊥DF于G,連結AG,
由三垂線定理得AG⊥DF,
∴∠AGH是二面角A-DF-B的平面角.
∵AH=![]() ,AG=
,AG=![]() ,
,
∴sin∠AGH=![]() .
.
∴∠AGH=60°.
∴二面角ADFB的大小為60°.
解法二:(1)證明:建立如圖所示的空間直角坐標系.
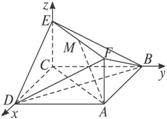
設AC∩BD=N,連結NE,則點N、E的坐標分別是(![]() ,
,![]() ,0)、(0,0,1),
,0)、(0,0,1),
∴![]() =(-
=(-![]() ,-
,-![]() ,1).
,1).
又點A、M的坐標分別是(![]() ,
,![]() ,0)、(
,0)、( ![]() ,
,![]() ,1),
,1),
∴![]() =(-
=(-![]() ,-
,-![]() ,1).
,1).
∴![]() =
=![]() 且
且![]() 與
與![]() 不共線.
不共線.
∴NE∥AM.
又∵NE![]() 平面BDE,AM
平面BDE,AM![]() 平面BDE,
平面BDE,
∴AM∥平面BDE.
(2)證明: ![]() =(-
=(-![]() ,-
,-![]() ,1),
,1),
∵D(![]() ,0,0),F(
,0,0),F(![]() ,
,![]() ,1),∴DF=(0,
,1),∴DF=(0, ![]() ,1).
,1).
∴![]() ·
·![]() =0.∴
=0.∴![]() ⊥
⊥![]() .
.
同理, ![]() ⊥
⊥![]() .又DF∩BF=F,
.又DF∩BF=F,
∴AM⊥平面BDF.
(3)解:∵AF⊥AB,AB⊥AD,AF∩AD=A,
∴AB⊥平面ADF.
∴![]() =(
=(![]() ,0,0)為平面ADF的法向量.
,0,0)為平面ADF的法向量.
∵![]() ·
·![]() =(
=(![]() ,
,![]() ,1)·(
,1)·(![]() ,
,![]() ,0)=0,
,0)=0,
![]() ·
·![]() =(
=(![]() ,
,![]() ,1)·(
,1)·(![]() ·
·![]() ,1)=0,
,1)=0,
得![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() 為平面BDF的法向量.
為平面BDF的法向量.
∴cos〈![]() ,
, ![]() 〉=
〉=![]() .
.
∴![]() 與
與![]() 的夾角是60°,
的夾角是60°,
即求二面角ADFB的大小是60°.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源: 題型:
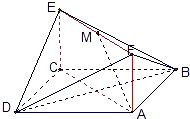 如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如圖,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=| 2 |
| 2 |
| ME |
| FM |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•深圳二模)如圖,已知正方形ABCD在水平面上的正投影(投影線垂直于投影面)是四邊形A′B′C′D′,其中A與A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如圖,已知正方形ABCD在水平面上的正投影(投影線垂直于投影面)是四邊形A′B′C′D′,其中A與A'重合,且BB′<DD′<CC′.| 2 |
| 5 |
| 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com