
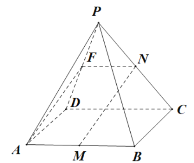
【題目】如圖所示,已知點(diǎn)P是![]() 所在平面外一點(diǎn),M,N,K分別AB,PC,PA的中點(diǎn),平面
所在平面外一點(diǎn),M,N,K分別AB,PC,PA的中點(diǎn),平面![]() 平面
平面![]() .
.

(1)求證:![]() 平面PAD;
平面PAD;
(2)直線(xiàn)PB上是否存在點(diǎn)H,使得平面![]() 平面ABCD,并加以證明;
平面ABCD,并加以證明;
(3)求證:![]() .
.
【答案】(1)見(jiàn)解析;(2)見(jiàn)解析;(3)見(jiàn)解析
【解析】
(1)利用線(xiàn)面平行的判定定理證明即可;
(2)利用面面平行的判定定理證明即可;
(3)利用線(xiàn)面平行的判定定理證明![]() 平面
平面![]() ,再由線(xiàn)面平行的性質(zhì)定理證明即可.
,再由線(xiàn)面平行的性質(zhì)定理證明即可.
(1)取![]() 中點(diǎn)為
中點(diǎn)為![]() ,連接
,連接![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
所以![]() ,即四邊形
,即四邊形![]() 為平行四邊形
為平行四邊形
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]()
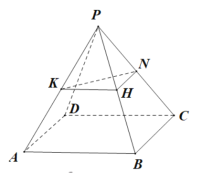
(2)當(dāng)![]() 為
為![]() 中點(diǎn)時(shí),平面
中點(diǎn)時(shí),平面![]() 平面
平面![]()
證明如下:
取![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,連接
,連接![]()
在![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() ,同理可證,
,同理可證,![]() 平面
平面![]()
又![]() 平面
平面![]() ,
,![]()
所以平面![]() 平面
平面![]()
(3)![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
又![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
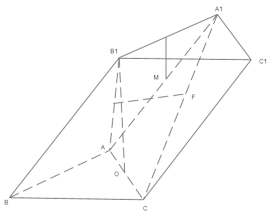
【題目】如圖,在三棱柱![]() 中,底面為邊長(zhǎng)為
中,底面為邊長(zhǎng)為![]() 的正三角形,
的正三角形,![]() 在底面的射影為
在底面的射影為![]() 中點(diǎn)且
中點(diǎn)且![]() 到底面的距離為
到底面的距離為![]() ,已知
,已知![]() 分別是線(xiàn)段
分別是線(xiàn)段![]() 與
與![]() 上的動(dòng)點(diǎn),記線(xiàn)段
上的動(dòng)點(diǎn),記線(xiàn)段![]() 中點(diǎn)
中點(diǎn)![]() 的軌跡為
的軌跡為![]() ,則
,則![]() 等于( )(注:
等于( )(注:![]() 表示
表示![]() 的測(cè)度,本題中
的測(cè)度,本題中![]() 若分別為曲線(xiàn)、平面圖形、空間幾何體,分別對(duì)應(yīng)為其長(zhǎng)度、面積、體積)
若分別為曲線(xiàn)、平面圖形、空間幾何體,分別對(duì)應(yīng)為其長(zhǎng)度、面積、體積)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2018年1月8日,中共中央國(guó)務(wù)院隆重舉行國(guó)家科學(xué)技術(shù)獎(jiǎng)勵(lì)大會(huì),在科技界引發(fā)熱烈反響,自主創(chuàng)新正成為引領(lǐng)經(jīng)濟(jì)社會(huì)發(fā)展的強(qiáng)勁動(dòng)力.某科研單位在研發(fā)新產(chǎn)品的過(guò)程中發(fā)現(xiàn)了一種新材料,由大數(shù)據(jù)測(cè)得該產(chǎn)品的性能指標(biāo)值y與這種新材料的含量x(單位:克)的關(guān)系為:當(dāng)![]() 時(shí),y是x的二次函數(shù);當(dāng)
時(shí),y是x的二次函數(shù);當(dāng)![]() 時(shí),
時(shí),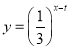 測(cè)得數(shù)據(jù)如下表(部分):
測(cè)得數(shù)據(jù)如下表(部分):
x(單位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y關(guān)于x的函數(shù)關(guān)系式![]() ;
;
(2)當(dāng)該產(chǎn)品中的新材料含量x為何值時(shí),產(chǎn)品的性能指標(biāo)值最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() (e為自然對(duì)數(shù)的底數(shù),e=2.71828……),函數(shù)
(e為自然對(duì)數(shù)的底數(shù),e=2.71828……),函數(shù)![]() 圖象關(guān)于直線(xiàn)
圖象關(guān)于直線(xiàn)![]() 對(duì)稱(chēng),函數(shù)
對(duì)稱(chēng),函數(shù)![]() 的最小值為m.
的最小值為m.
(I)求曲線(xiàn)![]() 的切線(xiàn)方程;
的切線(xiàn)方程;
(Ⅱ)求證:![]() ;
;
(III)求函數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】山東省于2015年設(shè)立了水下考古研究中心,以此推動(dòng)全省的水下考古、水下文化遺產(chǎn)保護(hù)等工作;水下考古研究中心工作站,分別設(shè)在位于劉公島的中國(guó)甲午戰(zhàn)爭(zhēng)博物院和威海市博物館。為對(duì)劉公島周邊海域水底情況進(jìn)行詳細(xì)了解,然后再選擇合適的時(shí)機(jī)下水探摸、打撈,省水下考古中心在一次水下考古活動(dòng)中,某一潛水員需潛水![]() 米到水底進(jìn)行考古作業(yè),其用氧量包含以下三個(gè)方面:
米到水底進(jìn)行考古作業(yè),其用氧量包含以下三個(gè)方面:
①下潛平均速度為![]() 米/分鐘,每分鐘的用氧量為
米/分鐘,每分鐘的用氧量為![]() 升;
升;
②水底作業(yè)時(shí)間范圍是最少10分鐘最多20分鐘,每分鐘用氧量為0.4升;
③返回水面時(shí),平均速度為![]() 米/分鐘,每分鐘用氧量為0.32升.
米/分鐘,每分鐘用氧量為0.32升.
潛水員在此次考古活動(dòng)中的總用氧量為![]() 升.
升.
(Ⅰ)如果水底作業(yè)時(shí)間是![]() 分鐘,將
分鐘,將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(Ⅱ)若![]() ,水底作業(yè)時(shí)間為20分鐘,求總用氧量
,水底作業(yè)時(shí)間為20分鐘,求總用氧量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列命題中正確的是( )
A.非零向量![]() 滿(mǎn)足
滿(mǎn)足![]() ,則
,則![]() 與
與![]() 的夾角為
的夾角為![]()
B.若![]() ,則
,則![]() 的夾角為銳角
的夾角為銳角
C.若![]() ,則
,則![]() 一定是直角三角形
一定是直角三角形
D.![]() 的外接圓的圓心為O,半徑為1,若
的外接圓的圓心為O,半徑為1,若![]() ,且
,且![]() ,則向量
,則向量![]() 在向量
在向量![]() 方向上的投影的數(shù)量為
方向上的投影的數(shù)量為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在如圖所示的平面直角坐標(biāo)系中,已知點(diǎn)A(1,0)和點(diǎn)B(﹣1,0),![]() ,且∠AOC=x,其中O為坐標(biāo)原點(diǎn).
,且∠AOC=x,其中O為坐標(biāo)原點(diǎn).

(1)若x=![]() ,設(shè)點(diǎn)D為線(xiàn)段OA上的動(dòng)點(diǎn),求
,設(shè)點(diǎn)D為線(xiàn)段OA上的動(dòng)點(diǎn),求![]() 的最小值;
的最小值;
(2)若![]() R,求
R,求![]() 的最大值及對(duì)應(yīng)的x值.
的最大值及對(duì)應(yīng)的x值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱錐P-ABC中,AC=BC=PC=2,AB=PA=PB=2![]() .
.
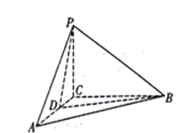
(1)證明:PC⊥平面ABC;
(2)若點(diǎn)D在棱AC上,且二面角D-PB-C為30°,求PD與平面PAB所成角的正弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正方體![]() 中.
中.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)試找出體對(duì)角線(xiàn)![]() 與平面
與平面![]() 和平面
和平面![]() 的交點(diǎn)
的交點(diǎn)![]() ,并證明:
,并證明:![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com