
【題目】已知雙曲線![]() 以
以![]() 為焦點,且過點
為焦點,且過點![]()
(1)求雙曲線![]() 與其漸近線的方程
與其漸近線的方程
(2)若斜率為1的直線![]() 與雙曲線
與雙曲線![]() 相交于
相交于![]() 兩點,且
兩點,且![]() (
(![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的方程
的方程
【答案】(1)雙曲線C的方程為![]() ; 漸近線方程為
; 漸近線方程為![]() .(2)l方程為
.(2)l方程為![]() .
.
【解析】
(1)設(shè)出雙曲線C方程,利用已知條件求出c,a,解得b,即可求出雙曲線方程與漸近線的方程;
(2)設(shè)直線l的方程為y=x+t,將其代入方程![]() ,通過△>0,求出t的范圍,設(shè)A(x1,y1),B(x2,y2),利用韋達定理,通過x1x2+y1y2=0,求解t即可得到直線方程.
,通過△>0,求出t的范圍,設(shè)A(x1,y1),B(x2,y2),利用韋達定理,通過x1x2+y1y2=0,求解t即可得到直線方程.
(1)設(shè)雙曲線C的方程為![]() ,半焦距為c,
,半焦距為c,
則c=2,![]() ,a=1,
,a=1,
所以b2=c2﹣a2=3,
故雙曲線C的方程為![]() .
.
雙曲線C的漸近線方程為![]() .
.
(2)設(shè)直線l的方程為y=x+t,將其代入方程![]() ,
,
可得2x2﹣2tx﹣t2﹣3=0(*)
△=4t2+8(t2+3)=12t2+24>0,若設(shè)A(x1,y1),B(x2,y2),
則x1,x2是方程(*)的兩個根,所以![]() ,
,
又由![]() ,可知x1x2+y1y2=0,
,可知x1x2+y1y2=0,
即x1x2+(x1+t)(x2+t)=0,可得![]() ,
,
故﹣(t2+3)+t2+t2=0,解得![]() ,
,
所以直線l方程為![]() .
.


 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 和
和![]() 滿足:
滿足:![]() ,且
,且![]() 成等比數(shù)列,
成等比數(shù)列,![]() 成等差數(shù)列.
成等差數(shù)列.
(1)行列式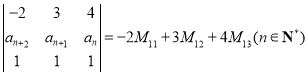 ,且
,且![]() ,求證:數(shù)列
,求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(2)在(1)的條件下,若![]() 不是常數(shù)列,
不是常數(shù)列,![]() 是等比數(shù)列,
是等比數(shù)列,
①求![]() 和
和![]() 的通項公式;
的通項公式;
②設(shè)![]() 是正整數(shù),若存在正整數(shù)
是正整數(shù),若存在正整數(shù)![]() ,使得
,使得![]() 成等差數(shù)列,求
成等差數(shù)列,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題中,正確的序號是_____
①直線上有兩個點到平面的距離相等,則這條直線和這個平面平行;
②過球面上任意兩點的大圓有且只有一個;
③直四棱柱是直平行六面體;
④![]() 為異面直線,則過
為異面直線,則過![]() 且與
且與![]() 平行的平面有且僅有一個;
平行的平面有且僅有一個;
⑤兩相鄰側(cè)面所成角相等的棱錐是正棱錐.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在萬眾創(chuàng)新的大經(jīng)濟背景下,某成都青年面包店推出一款新面包,每個面包的成本價為![]() 元,售價為
元,售價為![]() 元,該款面包當天只出一爐(一爐至少
元,該款面包當天只出一爐(一爐至少![]() 個,至多
個,至多![]() 個),當天如果沒有售完,剩余的面包以每個
個),當天如果沒有售完,剩余的面包以每個![]() 元的價格處理掉,為了確定這一爐面包的個數(shù),該店記錄了這款新面包最近
元的價格處理掉,為了確定這一爐面包的個數(shù),該店記錄了這款新面包最近![]() 天的日需求量(單位:個),整理得下表:
天的日需求量(單位:個),整理得下表:
日需求量 |
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
(1)根據(jù)表中數(shù)據(jù)可知,頻數(shù)![]() 與日需求量
與日需求量![]() (單位:個)線性相關(guān),求
(單位:個)線性相關(guān),求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)以![]() 天記錄的各日需求量的頻率代替各日需求量的概率,若該店這款新面包出爐的個數(shù)為
天記錄的各日需求量的頻率代替各日需求量的概率,若該店這款新面包出爐的個數(shù)為![]() ,記當日這款新面包獲得的總利潤為
,記當日這款新面包獲得的總利潤為![]() (單位:元).求
(單位:元).求![]() 的分布列及其數(shù)學期望.
的分布列及其數(shù)學期望.
相關(guān)公式: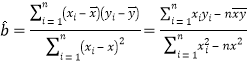 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,長度為2的線段EF的兩端點E、F分別在兩坐標軸上運動.
中,長度為2的線段EF的兩端點E、F分別在兩坐標軸上運動.
(1)求線段EF的中點G的軌跡C的方程;
(2)設(shè)軌跡C與![]() 軸交于
軸交于![]() 兩點,P是軌跡C上異于
兩點,P是軌跡C上異于![]() 的任意一點,直線
的任意一點,直線![]() 交直線
交直線![]() 于M點,直線
于M點,直線![]() 交直線
交直線![]() 于N點,求證:以MN為直徑的圓C總過定點,并求出定點坐標.
于N點,求證:以MN為直徑的圓C總過定點,并求出定點坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 分別是雙曲線E:
分別是雙曲線E: ![]()
![]() 的左、右焦點,P是雙曲線上一點,
的左、右焦點,P是雙曲線上一點, ![]() 到左頂點的距離等于它到漸近線距離的2倍,(1)求雙曲線的漸近線方程;(2)當
到左頂點的距離等于它到漸近線距離的2倍,(1)求雙曲線的漸近線方程;(2)當![]() 時,
時, ![]() 的面積為
的面積為![]() ,求此雙曲線的方程。
,求此雙曲線的方程。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】 已知函數(shù)![]() .
.
(1)求函數(shù)![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)已知函數(shù)![]() 區(qū)間
區(qū)間![]() 上的最小值為1,求實數(shù)
上的最小值為1,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(1)用行列式判斷關(guān)于![]() 的二元一次方程組
的二元一次方程組![]() 解的情況;
解的情況;
(2)用行列試解關(guān)于![]() 的二元一次方程組
的二元一次方程組![]() 并對解的情況進行討論.
并對解的情況進行討論.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com