
如果數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 ,那么這個(gè)數(shù)列的通項(xiàng)公式是 ( )
,那么這個(gè)數(shù)列的通項(xiàng)公式是 ( )
A. | B. |
C. | D.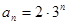 |
D
解析試題分析: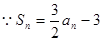 ,
,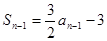 ,
,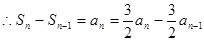 ,即:
,即: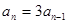
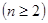 .
.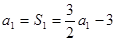 ,解得:
,解得: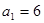 ,故
,故 是以
是以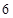 為首項(xiàng),公比為
為首項(xiàng),公比為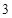 的等比數(shù)列,所以
的等比數(shù)列,所以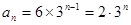
故選D.
考點(diǎn):數(shù)列的通項(xiàng)公式的求法



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
平面內(nèi)動(dòng)點(diǎn)P到點(diǎn)F(1,0)的距離等于它到直線(xiàn)x=-1的距離,記點(diǎn)P的軌跡為曲線(xiàn)Γ.
(1)求曲線(xiàn)Γ的方程;
(2)若點(diǎn)A,B,C是Γ上的不同三點(diǎn),且滿(mǎn)足 +
+ +
+ =0,證明:△ABC不可能為直角三角形.
=0,證明:△ABC不可能為直角三角形.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
已知數(shù)列{an}滿(mǎn)足an = nkn(n∈N*,0 < k < 1),下面說(shuō)法正確的是( )
①當(dāng) 時(shí),數(shù)列{an}為遞減數(shù)列;
時(shí),數(shù)列{an}為遞減數(shù)列;
②當(dāng) 時(shí),數(shù)列{an}不一定有最大項(xiàng);
時(shí),數(shù)列{an}不一定有最大項(xiàng);
③當(dāng)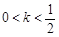 時(shí),數(shù)列{an}為遞減數(shù)列;
時(shí),數(shù)列{an}為遞減數(shù)列;
④當(dāng)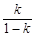 為正整數(shù)時(shí),數(shù)列{an}必有兩項(xiàng)相等的最大項(xiàng).
為正整數(shù)時(shí),數(shù)列{an}必有兩項(xiàng)相等的最大項(xiàng).
| A.①② | B.②④ | C.③④ | D.②③ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
數(shù)列 ,3,
,3, ,
, ,
, ,…,則9是這個(gè)數(shù)列的第( )
,…,則9是這個(gè)數(shù)列的第( )
| A.12項(xiàng) | B.13項(xiàng) | C.14項(xiàng) | D.15項(xiàng) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
如圖,在由二項(xiàng)式系數(shù)所構(gòu)成的楊輝三角形中,
若第 行中從左至右第
行中從左至右第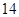 與第
與第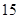 個(gè)數(shù)的比為
個(gè)數(shù)的比為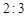 ,
,
則 的值為
的值為
A.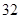 | B.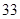 |
C.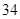 | D. |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
數(shù)列1,2,4,8,16,32,…的一個(gè)通項(xiàng)公式是( )
| A.a(chǎn)n=2n-1 | B.a(chǎn)n= | C.a(chǎn)n= | D.a(chǎn)n= |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
.定義:在數(shù)列{an}中,an>0且an≠1,若
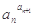 為定值,則稱(chēng)數(shù)列{an}為“等冪數(shù)列”.已知數(shù)列{an}為“等冪數(shù)列”,且a1=2,a2=4,Sn為數(shù)列{an}的前n項(xiàng)和,則S2009= ( )
為定值,則稱(chēng)數(shù)列{an}為“等冪數(shù)列”.已知數(shù)列{an}為“等冪數(shù)列”,且a1=2,a2=4,Sn為數(shù)列{an}的前n項(xiàng)和,則S2009= ( )
| A.6026 | B.6024 | C.2 | D.4 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com