
【題目】函數![]() 且
且![]()
(1)當![]() 時,求函數
時,求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)定義在R上的函數![]() 滿足
滿足![]() ,當
,當![]() 時,
時,![]() 。若存在
。若存在![]() 滿足不等式
滿足不等式![]() 且
且![]() 是函數
是函數![]() 的一個零點,求實數a的取值范圍。
的一個零點,求實數a的取值范圍。
【答案】(1)![]() (2)
(2)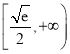
【解析】
(1)將![]() 代入
代入![]() ,求其導函數,得
,求其導函數,得![]() 的值,進而可得切線方程。
的值,進而可得切線方程。
(2)構造函數![]() ,根據已知得到其是奇函數,求導可得
,根據已知得到其是奇函數,求導可得![]() 在
在![]() 上的單調性,將
上的單調性,將![]() 轉化為關于
轉化為關于![]() 的不等式,利用
的不等式,利用![]() 的單調性解該不等式,可求得
的單調性解該不等式,可求得![]() 的范圍,即
的范圍,即![]() 的零點的范圍,轉化為
的零點的范圍,轉化為![]() 在
在![]() 的范圍上有零點,利用導數知識和零點存在性定理,可求出a的取值范圍。
的范圍上有零點,利用導數知識和零點存在性定理,可求出a的取值范圍。
解:(1)當![]() 時,因為
時,因為![]()
所以![]() ,
,
所以![]() ,
,
又![]() ,所以函數
,所以函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,
,
即![]()
(2)令![]() ,因為
,因為![]() ,
,
所以![]() ,
,
所以![]() 為奇函數。
為奇函數。
當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() 在R上單調遞減,
在R上單調遞減,
又![]() 滿足不等式
滿足不等式![]() ,即
,即![]() ,
,
所以![]() ,
,
化簡得![]() ,所以
,所以![]() ,即
,即![]()
令![]()
因為![]() 是函數
是函數![]() 的一個零點,
的一個零點,
所以![]() 在
在![]() 時有一個零點:
時有一個零點:
當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,
上單調遞減,
又![]() ,又因為
,又因為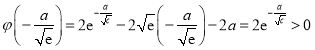 ,
,
所以要使![]() 在
在![]() 時有一個零點,只需
時有一個零點,只需![]() ,解得
,解得![]() ,
,
所以實數a的取值范圍為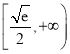


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:高中數學 來源: 題型:
【題目】某地區實施“光盤行動”以后,某自助啤酒吧也制定了自己的行動計劃,進店的每一位客人需預交![]() 元,啤酒根據需要自己用量杯量取,結賬時,根據每桌剩余酒量,按一定倍率收費(如下表),每桌剩余酒量不足
元,啤酒根據需要自己用量杯量取,結賬時,根據每桌剩余酒量,按一定倍率收費(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升計算(如剩余
升計算(如剩余![]() 升,記為剩余
升,記為剩余![]() 升).例如:結賬時,某桌剩余酒量恰好為
升).例如:結賬時,某桌剩余酒量恰好為![]() 升,則該桌的每位客人還應付
升,則該桌的每位客人還應付![]() 元.統計表明飲酒量與人數有很強的線性相關關系,下面是隨機采集的
元.統計表明飲酒量與人數有很強的線性相關關系,下面是隨機采集的![]() 組數據
組數據![]() (其中
(其中![]() 表示飲酒人數,
表示飲酒人數,![]() (升)表示飲酒量):
(升)表示飲酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(單位:升) |
|
|
|
|
|
結賬時的倍率 |
|
|
|
|
|
(1)求由這![]() 組數據得到的
組數據得到的![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(2)小王約了![]() 位朋友坐在一桌飲酒,小王及朋友用量杯共量取了
位朋友坐在一桌飲酒,小王及朋友用量杯共量取了![]() 升啤酒,這時,酒吧服務生對小王說,根據他的經驗,小王和朋友量取的啤酒可能喝不完,可以考慮再邀請
升啤酒,這時,酒吧服務生對小王說,根據他的經驗,小王和朋友量取的啤酒可能喝不完,可以考慮再邀請![]() 位或
位或![]() 位朋友一起來飲酒,會更劃算.試向小王是否該接受服務生的建議?
位朋友一起來飲酒,會更劃算.試向小王是否該接受服務生的建議?
參考數據:回歸直線的方程是![]() ,其中
,其中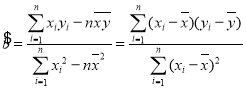 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中a的值;
(Ⅱ)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某冰糖橙,甜橙的一種,云南著名特產,以味甜皮薄著稱。該橙按照等級可分為四類:珍品、特級、優級和一級(每箱有5kg),某采購商打算訂購一批橙子銷往省外,并從采購的這批橙子中隨機抽取100箱,利用橙子的等級分類標準得到的數據如下表:
等級 | 珍品 | 特級 | 優級 | 一級 |
箱數 | 40 | 30 | 10 | 20 |
(1)若將頻率改為概率,從這100箱橙子中有放回地隨機抽取4箱,求恰好抽到2箱是一級品的概率:
(2)利用樣本估計總體,莊園老板提出兩種購銷方案供采購商參考:
方案一:不分等級賣出,價格為27元/kg;
方案二:分等級賣出,分等級的橙子價格如下:
等級 | 珍品 | 特級 | 優級 | 一級 |
售價(元/kg) | 36 | 30 | 24 | 18 |
從采購商的角度考慮,應該采用哪種方案?
(3)用分層抽樣的方法從這100箱橙子中抽取10箱,再從抽取的10箱中隨機抽取3箱,X表示抽取的是珍品等級,求x的分布列及數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)證明:![]() 面
面![]() ;
;
(2)在![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ,若存在,請計算
,若存在,請計算![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(3)若![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,且
,且![]() 平面
平面![]() ,
,![]() ,M,N分別為
,M,N分別為![]() ,
,![]() 的中點.
的中點.

(1)記平面![]() 與底面
與底面![]() 的交線為l,試判斷直線l與平面
的交線為l,試判斷直線l與平面![]() 的位置關系,并證明.
的位置關系,并證明.
(2)點Q在棱![]() 上,若Q到平面
上,若Q到平面![]() 的距離為
的距離為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高鐵站停車場針對小型機動車收費標準如下:2小時內(含2小時)每輛每次收費5元;超過2小時不超過5小時,每增加一小時收費增加3元,不足一小時的按一小時計費;超過5小時至24小時內(含24小時)收費15元封頂。超過24小時,按前述標準重新計費.為了調查該停車場一天的收費情況,現統計1000輛車的停留時間(假設每輛車一天內在該停車場僅停車一次),得到下面的頻數分布表:
T(小時) |
|
|
|
|
|
頻數(車次) | 600 | 120 | 80 | 100 | 100 |
以車輛在停車場停留時間位于各區間的頻率代替車輛在停車場停留時間位于各區間的概率。
(1)X表示某輛車在該停車場停車一次所交費用,求X的概率分布列及期望![]() ;
;
(2)現隨機抽取該停車場內停放的3輛車,![]() 表示3輛車中停車費用少于
表示3輛車中停車費用少于![]() 的車輛數,求
的車輛數,求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com