
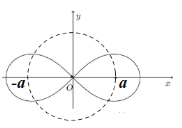
【題目】雙紐線最早于1694年被瑞士數(shù)學(xué)家雅各布·伯努利用來描述他所發(fā)現(xiàn)的曲線.在平面直角坐標(biāo)系![]() 中,把到定點
中,把到定點![]() ,
,![]() 距離之積等于
距離之積等于![]() (
(![]() )的點的軌跡稱為雙紐線C.已知點
)的點的軌跡稱為雙紐線C.已知點![]() 是雙紐線C上一點,下列說法中正確的有( )
是雙紐線C上一點,下列說法中正確的有( )
①雙紐線C關(guān)于原點O中心對稱; ②![]() ;
;
③雙紐線C上滿足![]() 的點P有兩個; ④
的點P有兩個; ④![]() 的最大值為
的最大值為![]() .
.
A.①②B.①②④C.②③④D.①③
【答案】B
【解析】
對①,設(shè)動點![]() ,把
,把![]() 關(guān)于原點對稱的點
關(guān)于原點對稱的點![]() 代入軌跡方程,顯然成立;
代入軌跡方程,顯然成立;
對②,根據(jù)![]() 的面積范圍證明即可.
的面積范圍證明即可.
對③,易得若![]() 則
則![]() 在
在![]() 軸上,再根據(jù)
軸上,再根據(jù)![]() 的軌跡方程求解即可.
的軌跡方程求解即可.
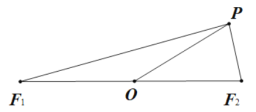
對④,根據(jù)題中所給的定點![]() ,
,![]() 距離之積等于
距離之積等于![]() ,再畫圖利用余弦定理分析
,再畫圖利用余弦定理分析![]() 中的邊長關(guān)系,進而利用三角形三邊的關(guān)系證明即可.
中的邊長關(guān)系,進而利用三角形三邊的關(guān)系證明即可.
對①,設(shè)動點![]() ,由題可得
,由題可得![]() 的軌跡方程
的軌跡方程![]() ,把
,把![]() 關(guān)于原點對稱的點
關(guān)于原點對稱的點![]() 代入軌跡方程顯然成立.故①正確;
代入軌跡方程顯然成立.故①正確;
對②,因為![]() ,故
,故![]() .
.
又![]() ,所以
,所以![]() ,
,
即![]() ,故
,故![]() .故②正確;
.故②正確;
對③, 若![]() 則
則![]() 在
在![]() 的中垂線即
的中垂線即![]() 軸上.
軸上.
故此時![]() ,代入
,代入![]() ,
,
可得![]() ,即
,即![]() ,僅有一個.故③錯誤;
,僅有一個.故③錯誤;
對④,因為![]() ,故
,故![]() ,
,
即![]() ,
,
因為![]() ,
,![]()
故![]() .
.
即![]() ,
,
所以![]() .
.
又![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 共線時取等號.
共線時取等號.
故![]() ,
,
即![]() ,解得
,解得![]() .故④正確.
.故④正確.
故①②④正確.
故選:B


 新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案
新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案 藍天教育暑假優(yōu)化學(xué)習(xí)系列答案
藍天教育暑假優(yōu)化學(xué)習(xí)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() :
:![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),曲線
),曲線![]() :
:![]() (
(![]() 為參數(shù)),
為參數(shù)),![]() 與
與![]() 相切于點
相切于點![]() ,以坐標(biāo)原點為極點,
,以坐標(biāo)原點為極點,![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系.
軸的非負(fù)半軸為極軸建立極坐標(biāo)系.
(1)求![]() 的極坐標(biāo)方程及點
的極坐標(biāo)方程及點![]() 的極坐標(biāo);
的極坐標(biāo);
(2)已知直線![]() :
:![]() 與圓
與圓![]() :
:![]() 交于
交于![]() ,
,![]() 兩點,記
兩點,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了保障某種藥品的主要藥理成分在國家藥品監(jiān)督管理局規(guī)定的值范圍內(nèi),某制藥廠在該藥品的生產(chǎn)過程中,檢驗員在一天中按照規(guī)定每間隔2小時對該藥品進行檢測,每天檢測4次:每次檢測由檢驗員從該藥品生產(chǎn)線上隨機抽取20件產(chǎn)品進行檢測,測量其主要藥理成分含量(單位:![]() )根據(jù)生產(chǎn)經(jīng)驗,可以認(rèn)為這條藥品生產(chǎn)線正常狀態(tài)下生產(chǎn)的產(chǎn)品的其主要藥理成分含量服從正態(tài)分布
)根據(jù)生產(chǎn)經(jīng)驗,可以認(rèn)為這條藥品生產(chǎn)線正常狀態(tài)下生產(chǎn)的產(chǎn)品的其主要藥理成分含量服從正態(tài)分布![]() .
.
(1)假設(shè)生產(chǎn)狀態(tài)正常,記![]() 表示某次抽取的20件產(chǎn)品中其主要藥理成分含量在
表示某次抽取的20件產(chǎn)品中其主要藥理成分含量在![]() 之外的藥品件數(shù),求
之外的藥品件數(shù),求![]() 的數(shù)學(xué)期望;
的數(shù)學(xué)期望;
(2)在一天的四次檢測中,如果有一次出現(xiàn)了主要藥理成分含量在![]() 之外的藥品,就認(rèn)為這條生產(chǎn)線在這一天的生產(chǎn)過程可能出現(xiàn)異常情況,需對本次的生產(chǎn)過程進行檢查;如果有兩次或兩次以上出現(xiàn)了主要藥理成分含量在
之外的藥品,就認(rèn)為這條生產(chǎn)線在這一天的生產(chǎn)過程可能出現(xiàn)異常情況,需對本次的生產(chǎn)過程進行檢查;如果有兩次或兩次以上出現(xiàn)了主要藥理成分含量在![]() 之外的藥品,則需停止生產(chǎn)并對原材料進行檢測.
之外的藥品,則需停止生產(chǎn)并對原材料進行檢測.
①下面是檢驗員在某次抽取的20件藥品的主要藥理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 10.05 | 10.05 | 9.96 | 10.12 |
經(jīng)計算得,![]() ,
, .其中
.其中![]() 為抽取的第
為抽取的第![]() 件藥品的主要藥理成分含量
件藥品的主要藥理成分含量![]() ,用樣本平均數(shù)
,用樣本平均數(shù)![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標(biāo)準(zhǔn)差
,用樣本標(biāo)準(zhǔn)差![]() 作為
作為![]() 的估計值
的估計值![]() ,利用估計值判斷是否需對本次的生產(chǎn)過程進行檢查?
,利用估計值判斷是否需對本次的生產(chǎn)過程進行檢查?
②試確定一天中需停止生產(chǎn)并對原材料進行檢測的概率(精確到0.001).
附:若隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點到直線
的焦點到直線![]() 的距離為
的距離為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
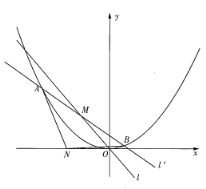
(2)如圖,若![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 兩點,與直線
兩點,與直線![]() 相交于點
相交于點![]() ,且
,且![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校對高一年級學(xué)生寒假參加社區(qū)服務(wù)的次數(shù)進行了統(tǒng)計,隨機抽取了![]() 名學(xué)生作為樣本,得到這
名學(xué)生作為樣本,得到這![]() 名學(xué)生參加社區(qū)服務(wù)的次數(shù),根據(jù)此數(shù)據(jù)作出了頻率分布統(tǒng)計表和頻率分布直方圖如下:
名學(xué)生參加社區(qū)服務(wù)的次數(shù),根據(jù)此數(shù)據(jù)作出了頻率分布統(tǒng)計表和頻率分布直方圖如下:

(1)求表中![]() 的值和頻率分布直方圖中
的值和頻率分布直方圖中![]() 的值,并根據(jù)頻率分布直方圖估計該校高一學(xué)生寒假參加社區(qū)服務(wù)次數(shù)的中位數(shù);
的值,并根據(jù)頻率分布直方圖估計該校高一學(xué)生寒假參加社區(qū)服務(wù)次數(shù)的中位數(shù);
(2)如果用分層抽樣的方法從樣本服務(wù)次數(shù)在![]() 和
和![]() 的人中共抽取6人,再從這6人中選2人,求2人服務(wù)次數(shù)都在
的人中共抽取6人,再從這6人中選2人,求2人服務(wù)次數(shù)都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】孫子定理是中國古代求解一次同余式組的方法,是數(shù)論中一個重要定理,最早可見于中國南北朝時期的數(shù)學(xué)著作《孫子算經(jīng)》,![]() 年英國來華傳教士偉烈亞力將其問題的解法傳至歐洲,
年英國來華傳教士偉烈亞力將其問題的解法傳至歐洲,![]() 年英國數(shù)學(xué)家馬西森指出此法符合
年英國數(shù)學(xué)家馬西森指出此法符合![]() 年由高斯得出的關(guān)于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.這個定理講的是一個關(guān)于整除的問題,現(xiàn)有這樣一個整除問題:將
年由高斯得出的關(guān)于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.這個定理講的是一個關(guān)于整除的問題,現(xiàn)有這樣一個整除問題:將![]() 至
至![]() 這
這![]() 個整數(shù)中能被
個整數(shù)中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的數(shù)按由小到大的順序排成一列構(gòu)成一數(shù)列,則此數(shù)列的項數(shù)是( )
的數(shù)按由小到大的順序排成一列構(gòu)成一數(shù)列,則此數(shù)列的項數(shù)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的傾斜角為
的傾斜角為![]() ,且經(jīng)過點
,且經(jīng)過點![]() ,以坐標(biāo)原點O為極點,
,以坐標(biāo)原點O為極點,![]() 軸正半軸為極軸建立極坐標(biāo)系,直線
軸正半軸為極軸建立極坐標(biāo)系,直線![]() ,從原點O作射線交
,從原點O作射線交![]() 于點M,點N為射線OM上的點,滿足|
于點M,點N為射線OM上的點,滿足| ![]() ,記點N的軌跡為曲線C.
,記點N的軌跡為曲線C.
(1)①設(shè)動點![]() ,記
,記![]() 是直線
是直線![]() 的向上方向的單位方向向量,且
的向上方向的單位方向向量,且![]() ,以t為參數(shù)求直線
,以t為參數(shù)求直線![]() 的參數(shù)方程
的參數(shù)方程
②求曲線C的極坐標(biāo)方程并化為直角坐標(biāo)方程;
(2)設(shè)直線![]() 與曲線C交于P,Q兩點,求
與曲線C交于P,Q兩點,求![]() 的值
的值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓![]() 的右頂點為A,上頂點為B.已知橢圓的離心率為
的右頂點為A,上頂點為B.已知橢圓的離心率為![]() ,
,![]() .
.
(1)求橢圓的方程;
(2)設(shè)直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,
兩點,![]() 與直線
與直線![]() 交于點M,且點P,M均在第四象限.若
交于點M,且點P,M均在第四象限.若![]() 的面積是
的面積是![]() 面積的2倍,求
面積的2倍,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com