
【題目】設(shè)函數(shù)![]() (
(![]() ).
).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若關(guān)于x的方程![]() 有唯一的實(shí)數(shù)解,求a的取值范圍.
有唯一的實(shí)數(shù)解,求a的取值范圍.
【答案】(1)當(dāng)![]() 時,
時,![]() 遞增區(qū)間時
遞增區(qū)間時![]() ,無遞減區(qū)間,當(dāng)
,無遞減區(qū)間,當(dāng)![]() 時,
時,![]() 遞增區(qū)間時
遞增區(qū)間時![]() ,遞減區(qū)間時
,遞減區(qū)間時![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)求出![]() ,對
,對![]() 分類討論,先考慮
分類討論,先考慮![]() (或
(或![]() )恒成立
)恒成立![]() 的范圍,并以此作為
的范圍,并以此作為![]() 的分類標(biāo)準(zhǔn),若不恒成立,求解
的分類標(biāo)準(zhǔn),若不恒成立,求解![]() ,即可得出結(jié)論;
,即可得出結(jié)論;
(2)![]() 有解,即
有解,即![]() ,令
,令![]() ,轉(zhuǎn)化求函數(shù)
,轉(zhuǎn)化求函數(shù)![]() 只有一個實(shí)數(shù)解,根據(jù)(1)中的結(jié)論,即可求解.
只有一個實(shí)數(shù)解,根據(jù)(1)中的結(jié)論,即可求解.
(1)![]() ,
,
當(dāng)![]() 時,
時,![]() 恒成立,
恒成立,
當(dāng)![]() 時,
時,![]() ,
,
綜上,當(dāng)![]() 時,
時,![]() 遞增區(qū)間時
遞增區(qū)間時![]() ,無遞減區(qū)間,
,無遞減區(qū)間,
當(dāng)![]() 時,
時,![]() 遞增區(qū)間時
遞增區(qū)間時![]() ,遞減區(qū)間時
,遞減區(qū)間時![]() ;
;
(2)![]() ,
,
![]()
令![]() ,原方程只有一個解,只需
,原方程只有一個解,只需![]() 只有一個解,
只有一個解,
即求![]() 只有一個零點(diǎn)時,
只有一個零點(diǎn)時,![]() 的取值范圍,
的取值范圍,
由(1)得當(dāng)![]() 時,
時,![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
且![]() ,函數(shù)只有一個零點(diǎn),原方程只有一個解
,函數(shù)只有一個零點(diǎn),原方程只有一個解![]() ,
,
當(dāng)![]() 時,由(1)得
時,由(1)得![]() 在
在![]() 出取得極小值,也是最小值,
出取得極小值,也是最小值,
當(dāng)![]() 時,
時,![]() ,此時函數(shù)只有一個零點(diǎn),
,此時函數(shù)只有一個零點(diǎn),
原方程只有一個解![]() ,
,
當(dāng)![]() 且
且![]()
遞增區(qū)間時![]() ,遞減區(qū)間時
,遞減區(qū)間時![]() ;
;
![]() ,當(dāng)
,當(dāng)![]() ,
,
![]() 有兩個零點(diǎn),
有兩個零點(diǎn),
即原方程有兩個解,不合題意,
所以![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某大型公司為了切實(shí)保障員工的健康安全,貫徹好衛(wèi)生防疫工作的相關(guān)要求,決定在全公司范圍內(nèi)舉行一次![]() 普查,為此需要抽驗(yàn)1000人的血樣進(jìn)行化驗(yàn),由于人數(shù)較多,檢疫部門制定了下列兩種可供選擇的方案.方案①:將每個人的血分別化驗(yàn),這時需要驗(yàn)1000次.方案②:按
普查,為此需要抽驗(yàn)1000人的血樣進(jìn)行化驗(yàn),由于人數(shù)較多,檢疫部門制定了下列兩種可供選擇的方案.方案①:將每個人的血分別化驗(yàn),這時需要驗(yàn)1000次.方案②:按![]() 個人一組進(jìn)行隨機(jī)分組,把從每組
個人一組進(jìn)行隨機(jī)分組,把從每組![]() 個人抽來的血混合在一起進(jìn)行檢驗(yàn),如果每個人的血均為陰性,則驗(yàn)出的結(jié)果呈陰性,這
個人抽來的血混合在一起進(jìn)行檢驗(yàn),如果每個人的血均為陰性,則驗(yàn)出的結(jié)果呈陰性,這![]() 個人的血只需檢驗(yàn)一次(這時認(rèn)為每個人的血化驗(yàn)
個人的血只需檢驗(yàn)一次(這時認(rèn)為每個人的血化驗(yàn)![]() 次);否則,若呈陽性,則需對這
次);否則,若呈陽性,則需對這![]() 個人的血樣再分別進(jìn)行一次化驗(yàn),這樣,該組
個人的血樣再分別進(jìn)行一次化驗(yàn),這樣,該組![]() 個人的血總共需要化驗(yàn)
個人的血總共需要化驗(yàn)![]() 次.假設(shè)此次普查中每個人的血樣化驗(yàn)呈陽性的概率為
次.假設(shè)此次普查中每個人的血樣化驗(yàn)呈陽性的概率為![]() ,且這些人之間的試驗(yàn)反應(yīng)相互獨(dú)立.
,且這些人之間的試驗(yàn)反應(yīng)相互獨(dú)立.
(1)設(shè)方案②中,某組![]() 個人的每個人的血化驗(yàn)次數(shù)為
個人的每個人的血化驗(yàn)次數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(2)設(shè)![]() ,試比較方案②中,分別取2,3,4時,各需化驗(yàn)的平均總次數(shù);并指出在這三種分組情況下,相比方案①,化驗(yàn)次數(shù)最多可以平均減少多少次?(最后結(jié)果四舍五入保留整數(shù))
,試比較方案②中,分別取2,3,4時,各需化驗(yàn)的平均總次數(shù);并指出在這三種分組情況下,相比方案①,化驗(yàn)次數(shù)最多可以平均減少多少次?(最后結(jié)果四舍五入保留整數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,長為3的線段的兩端點(diǎn)
中,長為3的線段的兩端點(diǎn)![]() 分別在
分別在![]() 軸、
軸、![]() 軸上滑動,點(diǎn)
軸上滑動,點(diǎn)![]() 為線段
為線段![]() 上的點(diǎn),且滿足
上的點(diǎn),且滿足![]() .記點(diǎn)
.記點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若點(diǎn)![]() 為曲線
為曲線![]() 上的兩個動點(diǎn),記
上的兩個動點(diǎn),記![]() ,判斷是否存在常數(shù)
,判斷是否存在常數(shù)![]() 使得點(diǎn)
使得點(diǎn)![]() 到直線
到直線![]() 的距離為定值?若存在,求出常數(shù)
的距離為定值?若存在,求出常數(shù)![]() 的值和這個定值;若不存在,請說明理由.
的值和這個定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種產(chǎn)品的質(zhì)量以其質(zhì)量指標(biāo)值衡量,并依據(jù)質(zhì)量指標(biāo)值劃分等級如下表:
![]()
從某企業(yè)生產(chǎn)的這種產(chǎn)品中抽取200件,檢測后得到如下的頻率分布直方圖:
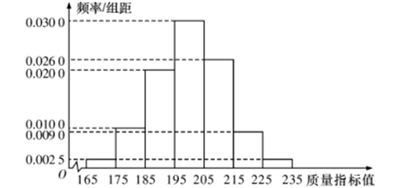
(1)根據(jù)以上抽樣調(diào)查數(shù)據(jù),能否認(rèn)為該企業(yè)生產(chǎn)的這種產(chǎn)品符合“一、二等品至少要占全部產(chǎn)品![]() ”的規(guī)定?
”的規(guī)定?
(2)在樣本中,按產(chǎn)品等級用分層抽樣的方法抽取8件,再從這8件產(chǎn)品中隨機(jī)抽取4件,求抽取的4件產(chǎn)品中,一、二、三等品都有的概率;
(3)該企業(yè)為提高產(chǎn)品質(zhì)量,開展了“質(zhì)量提升月”活動,活動后再抽樣檢測,產(chǎn)品質(zhì)量指標(biāo)值![]() 近似滿足
近似滿足![]() ,則“質(zhì)量提升月”活動后的質(zhì)量指標(biāo)值的均值比活動前大約提升了多少?
,則“質(zhì)量提升月”活動后的質(zhì)量指標(biāo)值的均值比活動前大約提升了多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,橢圓![]() 的離心率為
的離心率為![]() ,過橢圓右焦點(diǎn)
,過橢圓右焦點(diǎn)![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 與
與![]() .當(dāng)直線
.當(dāng)直線![]() 斜率為0時,
斜率為0時,![]() .
.
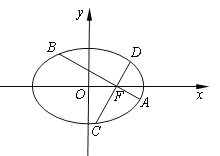
(1)求橢圓的方程;
(2)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為迎接2022年冬奧會,北京市組織中學(xué)生開展冰雪運(yùn)動的培訓(xùn)活動,并在培訓(xùn)結(jié)束后對學(xué)生進(jìn)行了考核.記![]() 表示學(xué)生的考核成績,并規(guī)定
表示學(xué)生的考核成績,并規(guī)定![]() 為考核優(yōu)秀.為了了解本次培訓(xùn)活動的效果,在參加培訓(xùn)的學(xué)生中隨機(jī)抽取了30名學(xué)生的考核成績,并作成如下莖葉圖:
為考核優(yōu)秀.為了了解本次培訓(xùn)活動的效果,在參加培訓(xùn)的學(xué)生中隨機(jī)抽取了30名學(xué)生的考核成績,并作成如下莖葉圖:

(Ⅰ)從參加培訓(xùn)的學(xué)生中隨機(jī)選取1人,請根據(jù)圖中數(shù)據(jù),估計這名學(xué)生考核優(yōu)秀的概率;
(Ⅱ)從圖中考核成績滿足![]() 的學(xué)生中任取2人,求至少有一人考核優(yōu)秀的概率;
的學(xué)生中任取2人,求至少有一人考核優(yōu)秀的概率;
(Ⅲ)記![]() 表示學(xué)生的考核成績在區(qū)間
表示學(xué)生的考核成績在區(qū)間![]() 的概率,根據(jù)以往培訓(xùn)數(shù)據(jù),規(guī)定當(dāng)
的概率,根據(jù)以往培訓(xùn)數(shù)據(jù),規(guī)定當(dāng)![]() 時培訓(xùn)有效.請根據(jù)圖中數(shù)據(jù),判斷此次中學(xué)生冰雪培訓(xùn)活動是否有效,并說明理由.
時培訓(xùn)有效.請根據(jù)圖中數(shù)據(jù),判斷此次中學(xué)生冰雪培訓(xùn)活動是否有效,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 中心在坐標(biāo)原點(diǎn),焦點(diǎn)在
中心在坐標(biāo)原點(diǎn),焦點(diǎn)在![]() 軸上,且過點(diǎn)
軸上,且過點(diǎn)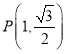 ,直線
,直線![]() 與橢圓交于
與橢圓交于![]() 兩點(diǎn)(
兩點(diǎn)(![]() 兩點(diǎn)不是左右頂點(diǎn)),若直線
兩點(diǎn)不是左右頂點(diǎn)),若直線![]() 的斜率為
的斜率為![]() 時,弦
時,弦![]() 的中點(diǎn)
的中點(diǎn)![]() 在直線
在直線![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若在橢圓上有相異的兩點(diǎn)![]() (
(![]() 三點(diǎn)不共線),
三點(diǎn)不共線),![]() 為坐標(biāo)原點(diǎn),且直線
為坐標(biāo)原點(diǎn),且直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率滿足
的斜率滿足![]() ,求證:
,求證:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列五個命題,其中正確命題的個數(shù)為( )
①命題“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”;
”;
②若正整數(shù)![]() 和
和![]() 滿足
滿足![]() ,則
,則![]() ;
;
③在![]() 中 ,
中 ,![]() 是
是![]() 的充要條件;
的充要條件;
④一條光線經(jīng)過點(diǎn)![]() ,射在直線
,射在直線![]() 上,反射后穿過點(diǎn)
上,反射后穿過點(diǎn)![]() ,則入射光線所在直線的方程為
,則入射光線所在直線的方程為![]() ;
;
⑤已知![]() 的三個零點(diǎn)分別為一橢圓、一雙曲線、一拋物線的離心率,則
的三個零點(diǎn)分別為一橢圓、一雙曲線、一拋物線的離心率,則![]() 為定值.
為定值.
A.2B.3C.4D.5
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知如圖1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D為AC中點(diǎn),AE![]() BD于E,延長AE交BC于F,將△ABD沿BD折起,使平面ABD
BD于E,延長AE交BC于F,將△ABD沿BD折起,使平面ABD![]() 平面BCD,如圖2所示。
平面BCD,如圖2所示。
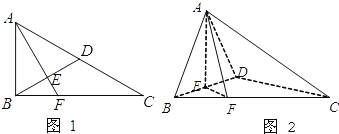
(Ⅰ)求證:AE![]() 平面BCD;
平面BCD;
(Ⅱ)求二面角A-DC-B的余弦值;
(Ⅲ)求三棱錐B-AEF與四棱錐A-FEDC的體積的比(只需寫出結(jié)果,不要求過程).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com