已知A、B為x軸上不同的兩點(diǎn)，點(diǎn)P的橫坐標(biāo)為1，且|PA|=|PB|，若直線(xiàn)PA的方程為x-y+1=0，則直線(xiàn)PB的方程為 （ ）
A．x+y-3=0
B．x+3y-7=0
C．x+y-5=0
D．2y-x-3=0
【答案】分析：利用直線(xiàn)PA的方程為x-y+1=0求出PA的斜率，根據(jù)|PA|=|PB|，求出PB的傾斜角，再求出P的坐標(biāo)，然后可求出直線(xiàn)PB的方程．
解答：解：由于直線(xiàn)PA的方程為x-y+1=0，∴直線(xiàn)PA的傾斜角為45°，
∵|PA|=|PB|，∴直線(xiàn)PB的傾斜角為135°，
又當(dāng)x=1時(shí)，y=2，即P（1，2），
∴直線(xiàn)PB的方程為y-2=-（x-1），即x+y-3=0．
故選A
點(diǎn)評(píng)：本題考查與直線(xiàn)關(guān)于點(diǎn)、直線(xiàn)對(duì)稱(chēng)的直線(xiàn)方程，考查邏輯推理能力，計(jì)算能力，轉(zhuǎn)化思想的應(yīng)用，是基礎(chǔ)題．
已知F是橢圓
已知A、B為橢圓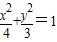
的左右頂點(diǎn)，F(xiàn)為橢圓的右焦點(diǎn)，P是橢圓上異于A、B的任意一點(diǎn)，直線(xiàn)AP、BP分別交直線(xiàn)l：x=m（m＞2）于M、N兩點(diǎn)，l交x軸于C點(diǎn)．