
【題目】設函數(shù)f(x)=ln(2x+3)+x2
(1)討論f(x)的單調(diào)性;
(2)求f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]的最大值和最小值.
]的最大值和最小值.
【答案】
(1)解:f(x)的定義域為(﹣ ![]() ,+∞)
,+∞)
f′(x)= ![]() +2x=
+2x= ![]()
當﹣ ![]() <x<﹣1時,f′(x)>0;
<x<﹣1時,f′(x)>0;
當﹣1<x<﹣ ![]() 時,f′(x)<0;
時,f′(x)<0;
當x>﹣ ![]() 時,f′(x)>0
時,f′(x)>0
從而,f(x)在區(qū)間(﹣ ![]() ,﹣1),(﹣
,﹣1),(﹣ ![]() ,+∞)上單調(diào)遞增,在區(qū)間(﹣1,﹣
,+∞)上單調(diào)遞增,在區(qū)間(﹣1,﹣ ![]() )上單調(diào)遞減
)上單調(diào)遞減
(2)解:f(x)的定義域為(﹣ ![]() ,+∞)
,+∞)
由(1)知f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]的最小值為f(﹣
]的最小值為f(﹣ ![]() )=ln2+
)=ln2+ ![]()
又f(﹣ ![]() )﹣f(
)﹣f( ![]() )=ln
)=ln ![]() +
+ ![]() ﹣ln
﹣ln ![]() ﹣
﹣ ![]()
=ln ![]() +
+ ![]() =
= ![]() (1﹣ln
(1﹣ln ![]() )<0
)<0
所以f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]的最大值為f(
]的最大值為f( ![]() )=
)= ![]() +ln
+ln ![]() .
.
【解析】(1)先根據(jù)對數(shù)定義求出函數(shù)的定義域,然后令f′(x)=0求出函數(shù)的穩(wěn)定點,當導函數(shù)大于0得到函數(shù)的增區(qū)間,當導函數(shù)小于0得到函數(shù)的減區(qū)間,即可得到函數(shù)的單調(diào)區(qū)間;(2)根據(jù)(1)知f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]的最小值為f(﹣
]的最小值為f(﹣ ![]() )求出得到函數(shù)的最小值,又因為f(﹣
)求出得到函數(shù)的最小值,又因為f(﹣ ![]() )﹣f(
)﹣f( ![]() )<0,得到f(x)在區(qū)間[﹣
)<0,得到f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]的最大值為f(
]的最大值為f( ![]() )求出得到函數(shù)的最大值.
)求出得到函數(shù)的最大值.
【考點精析】關于本題考查的利用導數(shù)研究函數(shù)的單調(diào)性和函數(shù)的最大(小)值與導數(shù),需要了解一般的,函數(shù)的單調(diào)性與其導數(shù)的正負有如下關系: 在某個區(qū)間![]() 內(nèi),(1)如果
內(nèi),(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞增;(2)如果
在這個區(qū)間單調(diào)遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞減;求函數(shù)
在這個區(qū)間單調(diào)遞減;求函數(shù)![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數(shù)
上的最大值與最小值的步驟:(1)求函數(shù)![]() 在
在![]() 內(nèi)的極值;(2)將函數(shù)
內(nèi)的極值;(2)將函數(shù)![]() 的各極值與端點處的函數(shù)值
的各極值與端點處的函數(shù)值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.
比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖1,在△ABC中, ![]() ,
, ![]() ,點D是BC的中點. ( I)求證:
,點D是BC的中點. ( I)求證: ![]() ;
;
( II)直線l過點D且垂直于BC,E為l上任意一點,求證: ![]() 為常數(shù),并求該常數(shù);
為常數(shù),并求該常數(shù);
( III)如圖2,若 ![]() ,F(xiàn)為線段AD上的任意一點,求
,F(xiàn)為線段AD上的任意一點,求 ![]() 的范圍.
的范圍.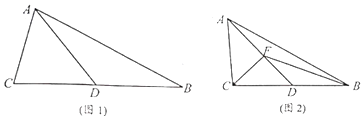
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC內(nèi)的一點.
,AC=3, BC=2,P是△ABC內(nèi)的一點.
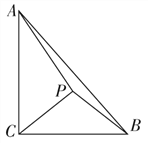
(1)若P是等腰直角三角形PBC的直角頂點,求PA的長;
(2)若∠BPC=![]() ,設∠PCB=θ,求△PBC的面積S(θ)的解析式,并求S(θ)的最大值.
,設∠PCB=θ,求△PBC的面積S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某著名歌星在某地舉辦一次歌友會,有1000人參加,每人一張門票,每張100元.在演出過程中穿插抽獎活動,第一輪抽獎從這1000張票根中隨機抽取10張,其持有者獲得價值1000元的獎品,并參加第二輪抽獎活動.第二輪抽獎由第一輪獲獎者獨立操作按鈕,電腦隨機產(chǎn)生兩個實數(shù)x,y(x,y∈[0,4]),若滿足y≥ ![]() ,電腦顯示“中獎”,則抽獎者再次獲得特等獎獎金;否則電腦顯示“謝謝”,則不獲得特等獎獎金.
,電腦顯示“中獎”,則抽獎者再次獲得特等獎獎金;否則電腦顯示“謝謝”,則不獲得特等獎獎金.
(1)已知小明在第一輪抽獎中被抽中,求小明在第二輪抽獎中獲獎的概率;
(2)設特等獎獎金為a元,小李是此次活動的顧客,求小李參加此次活動獲益的期望;若該歌友會組織者在此次活動中獲益的期望值是至少獲得70000元,求a的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】現(xiàn)需要設計一個倉庫,它由上下兩部分組成,上部分的形狀是正四棱錐![]() ,下部分的形狀是正四棱柱
,下部分的形狀是正四棱柱![]() (如圖所示),并要求正四棱柱的高
(如圖所示),并要求正四棱柱的高![]() 是正四棱錐的高
是正四棱錐的高![]() 的4倍.
的4倍.

(1)若![]() 則倉庫的容積是多少?
則倉庫的容積是多少?
(2)若正四棱錐的側(cè)棱長為![]() ,則當
,則當![]() 為多少時,倉庫的容積最大?
為多少時,倉庫的容積最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某公司為獲得較好的收益,每年要投入一定資金用于廣告促銷,經(jīng)調(diào)查,每年投入廣告費![]() (百萬元),可增加銷售額約為
(百萬元),可增加銷售額約為![]() (百萬元)(
(百萬元)(![]() )
)
(1)若該公司當年的廣告費控制在4百萬元之內(nèi),則應該設入多少廣告費,才能使該公司獲得的收益最大?
(2)現(xiàn)該公司準備共投入6百萬元,分別用于廣告促銷售和技術改造,經(jīng)預測,每設入技術改造費![]() (百萬元),可增加銷售額約為
(百萬元),可增加銷售額約為![]() (百萬元),請設計一種資金分配方案,使該公司由此獲得最大收益.(注:收益
(百萬元),請設計一種資金分配方案,使該公司由此獲得最大收益.(注:收益![]() 銷售額
銷售額![]() 成本)
成本)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() :
: ![]() 的焦點
的焦點![]() 與橢圓
與橢圓![]() :
: ![]() 的一個焦點重合,點
的一個焦點重合,點![]() 在拋物線上,過焦點
在拋物線上,過焦點![]() 的直線
的直線![]() 交拋物線于
交拋物線于![]() 、
、![]() 兩點.
兩點.
(Ⅰ)求拋物線![]() 的方程以及
的方程以及![]() 的值;
的值;
(Ⅱ)記拋物線的準線![]() 與
與![]() 軸交于點
軸交于點![]() ,試問是否存在常數(shù)
,試問是否存在常數(shù)![]() ,使得
,使得![]() 且
且![]() 都成立?若存在,求出實數(shù)
都成立?若存在,求出實數(shù)![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點P(2,0)及圓C:x2+y2﹣6x+4y+4=0.
(1)設過P直線l1與圓C交于M、N兩點,當|MN|=4時,求以MN為直徑的圓Q的方程;
(2)設直線ax﹣y+1=0與圓C交于A,B兩點,是否存在實數(shù)a,使得過點P(2,0)的直線l2垂直平分弦AB?若存在,求出實數(shù)a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,且sinA+![]() cosA=2.
cosA=2.
(Ⅰ)求角A的大小;
(Ⅱ)現(xiàn)給出三個條件:①a=2;②B=45°;③c= ![]() .試從中選出兩個可以確△ABC的條件,寫出你的選擇,并以此為依據(jù)求△ABC的面積.(只寫出一個方案即可)
.試從中選出兩個可以確△ABC的條件,寫出你的選擇,并以此為依據(jù)求△ABC的面積.(只寫出一個方案即可)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com