
【題目】數(shù)列{an}滿足a1=1,a2=2,an+2=![]() ,n=1,2,3,….求a3,a4,并求數(shù)列{an}的通項(xiàng)公式;
,n=1,2,3,….求a3,a4,并求數(shù)列{an}的通項(xiàng)公式;
【答案】見解析
【解析】試題分析:根據(jù)an+2=![]() ,把a1和a2代入即可求得a3, a4,先看當(dāng)n=2k-1時,整理得
,把a1和a2代入即可求得a3, a4,先看當(dāng)n=2k-1時,整理得![]() -
-![]() =1進(jìn)而可判斷數(shù)列{
=1進(jìn)而可判斷數(shù)列{![]() }是首項(xiàng)為1、公差為1的等差數(shù)列; n=2k時,整理得
}是首項(xiàng)為1、公差為1的等差數(shù)列; n=2k時,整理得![]() =2
=2![]() 進(jìn)而可判斷數(shù)列{
進(jìn)而可判斷數(shù)列{![]() }是首項(xiàng)為2、公比為2的等比數(shù)列,最后綜合可得答案.
}是首項(xiàng)為2、公比為2的等比數(shù)列,最后綜合可得答案.
試題解析:∵a1=1,a2=2,
∴a3=![]() =a1+1=2,
=a1+1=2,
a4=(![]() π)a2+
π)a2+![]() π=2a2=4,
π=2a2=4,
當(dāng)n=2k-1時,a2k+1=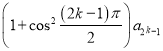 +
+
![]() =
=![]() +1,即
+1,即![]() -
-![]() =1,
=1,
所以數(shù)列{![]() }是首項(xiàng)為1,公差為1的等差數(shù)列,因此
}是首項(xiàng)為1,公差為1的等差數(shù)列,因此![]() =1+(k-1)=k,
=1+(k-1)=k,
當(dāng)n=2k時, ![]() =
=![]() +
+![]() =2
=2![]() ,
,
所以數(shù)列{![]() }是首項(xiàng)為2,公比為2的等比數(shù)列,因此
}是首項(xiàng)為2,公比為2的等比數(shù)列,因此![]() =
=![]() .
.
故數(shù)列{an}的通項(xiàng)公式為an=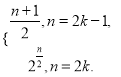



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,一智能掃地機(jī)器人在![]() 處發(fā)現(xiàn)位于它正西方向的
處發(fā)現(xiàn)位于它正西方向的![]() 處和北偏東30°方向上的
處和北偏東30°方向上的![]() 處分別有需要清掃的垃圾,紅外線感應(yīng)測量發(fā)現(xiàn)機(jī)器人到
處分別有需要清掃的垃圾,紅外線感應(yīng)測量發(fā)現(xiàn)機(jī)器人到![]() 的距離比到
的距離比到![]() 的距離少0.4米,于是選擇沿
的距離少0.4米,于是選擇沿![]() 路線清掃,已知智能掃地機(jī)器人的直線行走速度為0.2
路線清掃,已知智能掃地機(jī)器人的直線行走速度為0.2![]() ,忽略機(jī)器人吸入垃圾及在
,忽略機(jī)器人吸入垃圾及在![]() 處旋轉(zhuǎn)所用時間,10秒鐘完成了清掃任務(wù).
處旋轉(zhuǎn)所用時間,10秒鐘完成了清掃任務(wù).
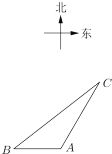
(1)![]() 、
、![]() 兩處垃圾的距離是多少?
兩處垃圾的距離是多少?
(2)智能掃地機(jī)器人此次清掃行走路線的夾角![]() 的正弦值是多少?
的正弦值是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠家具車間造![]() 、
、![]() 型兩類桌子,每張桌子需木工和漆工梁道工序完成.已知木工做一張
型兩類桌子,每張桌子需木工和漆工梁道工序完成.已知木工做一張![]() 、
、![]() 型型桌子分別需要1小時和2小時,漆工油漆一張
型型桌子分別需要1小時和2小時,漆工油漆一張![]() 、
、![]() 型型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張
型型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張![]() 、
、![]() 型型桌子分別獲利潤2千元和3千元.
型型桌子分別獲利潤2千元和3千元.
(1)列出滿足生產(chǎn)條件的數(shù)學(xué)關(guān)系式,并畫出可行域;
(2)怎樣分配生產(chǎn)任務(wù)才能使每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三課外興趣小組為了解高三同學(xué)高考結(jié)束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學(xué)生進(jìn)行問卷調(diào)查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中數(shù)據(jù)b,c;
(2)判斷是否有99%的把握認(rèn)為觀看2018年足球世界杯比賽與性別有關(guān);
(3)為了計算“從10人中選出9人參加比賽”的情況有多少種,我們可以發(fā)現(xiàn)它與“從10人中選出1人不參加比賽”的情況有多少種是一致的.現(xiàn)有問題:在打算觀看2018年足球世界杯比賽的同學(xué)中有5名男生、2名女生來自高三(5)班,從中推選5人接受校園電視臺采訪,請根據(jù)上述方法,求被推選出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 中,
中,![]() .
.
(1)求證:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(2)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)設(shè)![]() ,若對任意
,若對任意![]() ,有
,有![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(2015·浙江卷)已知數(shù)列{an}滿足a1=![]() 且an+1=an-
且an+1=an-![]() (n∈N*).
(n∈N*).
(1)證明:1≤![]() ≤2(n∈N*);
≤2(n∈N*);
(2)設(shè)數(shù)列{![]() }的前n項(xiàng)和為Sn,證明:
}的前n項(xiàng)和為Sn,證明: ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 是偶函數(shù),且滿足
是偶函數(shù),且滿足![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() 的最大值為
的最大值為![]() .
.
(1)求實(shí)數(shù)![]() 的值;
的值;
(2)函數(shù)![]() ,若對任意的
,若對任意的![]() ,總存在
,總存在![]() ,使不等式
,使不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com