
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)令![]() ,求函數
,求函數![]() 的極值;
的極值;
(3)若![]() ,正實數
,正實數![]() 滿足
滿足![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() (2)當
(2)當![]() 時,函數
時,函數![]() 無極值;當
無極值;當![]() 時,函數
時,函數![]() 有極大值
有極大值![]() ,無極小值(3)詳見解析
,無極小值(3)詳見解析
【解析】
試題分析:(1)由導數幾何意義得切線斜率![]() ,所以先求導數得
,所以先求導數得![]() ,即
,即![]() ,又
,又![]() ,再根據點斜式得切線方程
,再根據點斜式得切線方程![]() (2)先求導數
(2)先求導數![]() ,再分類討論導函數在定義區間上符號變化規律,確定極值取法:當
,再分類討論導函數在定義區間上符號變化規律,確定極值取法:當![]() 時,
時,![]() ,函數
,函數![]() 無極值點.當
無極值點.當![]() 時,一個零點
時,一個零點![]() ,導函數在其左右符號變化,先增后減,所以
,導函數在其左右符號變化,先增后減,所以![]() 有極大值,無極小值
有極大值,無極小值
(3)先化簡![]() 為
為![]() ,轉化為關于
,轉化為關于![]() 函數關系式:
函數關系式:![]() ,研究函數
,研究函數![]() ,其中
,其中![]() ,得
,得![]() ,因此
,因此![]() ,解不等式得
,解不等式得![]()
試題解析:(1)當![]() 時,
時,![]() ,則
,則![]() ,所以切點為
,所以切點為![]() ,
,
又![]() ,則切線斜率
,則切線斜率![]() ,
,
故切線方程為![]() ,即
,即![]() ................3分
................3分
(2)![]() ,
,
則![]() ,......................4分
,......................4分
當![]() 時,∵
時,∵![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 上是遞增函數,函數
上是遞增函數,函數![]() 無極值點..................5分
無極值點..................5分
當![]() 時,
時,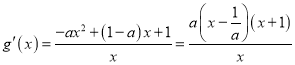 ,令
,令![]() 得
得![]() ,
,
∴當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
因此![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數,............................7分
上是減函數,............................7分
∴![]() 時,
時,![]() 有極大值
有極大值![]() ,
,
綜上,當![]() 時,函數
時,函數![]() 無極值;
無極值;
當![]() 時,函數
時,函數![]() 有極大值
有極大值![]() ,無極小值............................... 8分
,無極小值............................... 8分
(3)證明:當![]() 時,
時,![]() ,
,
由![]() ,即
,即![]() ,
,
從而![]() ,
,
令![]() ,則由
,則由![]() 得:
得:![]() ,
,
可知,![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增,
上單調遞增,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .....................12分
.....................12分


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】一個袋中裝有四個形狀大小完全相同的球,球的編號分別為1,2,3,4.
(1)從袋中隨機取出兩個球,求取出的球的編號之和不大于4的概率.
(2)先從袋中隨機取一個球,該球的編號為m,將球放回袋中,然后再從袋中隨機取一個球,該球的編號為n,求n<m+2的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() .
.
(1)若函數![]() 在
在![]() 上為增函數,求
上為增函數,求![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 在
在![]() 上不單調時;
上不單調時;
①記![]() 在
在![]() 上的最大值、最小值分別為
上的最大值、最小值分別為![]() ,求
,求![]() ;
;
②設![]() ,若
,若![]() ,對
,對![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于![]() 的二次函數
的二次函數![]() .
.
(1)設集合![]() 和
和![]() ,分別從集合
,分別從集合![]() 和
和![]() 中隨機取一個數作為
中隨機取一個數作為![]() 和
和![]() ,求函數
,求函數![]() 在區間
在區間![]() 上是增函數的概率;
上是增函數的概率;
(2)設點![]() 是區域
是區域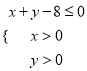 內的隨機點,記事件“函數
內的隨機點,記事件“函數![]() 有兩個零點,其中一個大于1,另一個小于1”為事件
有兩個零點,其中一個大于1,另一個小于1”為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
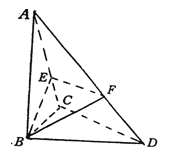
【題目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分別是AC、AD上的動點,且![]()
(1)求證:不論![]() 為何值,總有平面BEF⊥平面ABC;
為何值,總有平面BEF⊥平面ABC;
(2)當λ為何值時,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]()
![]() 的離心率為
的離心率為![]() ,
,![]() 是橢圓的右焦點,直線
是橢圓的右焦點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(I)求![]() 的方程;
的方程;
(II)設過點![]() 的動直線
的動直線![]() 與
與![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求
的面積最大時,求![]() 的方程
的方程
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方程![]() .
.
(1)求該方程表示一條直線的條件;
(2)當![]() 為何實數時,方程表示的直線斜率不存在?求出這時的直線方程;
為何實數時,方程表示的直線斜率不存在?求出這時的直線方程;
(3)已知方程表示的直線![]() 在
在![]() 軸上的截距為-3,求實數
軸上的截距為-3,求實數![]() 的值;
的值;
(4)若方程表示的直線![]() 的傾斜角是45°,求實數
的傾斜角是45°,求實數![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com