
已知二次函數(shù)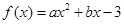 在
在 處取得極值,且在
處取得極值,且在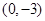 點處的切線與直線
點處的切線與直線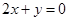 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函數(shù)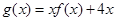 的單調(diào)遞增區(qū)間及極值。
的單調(diào)遞增區(qū)間及極值。
(3)求函數(shù)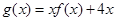 在
在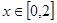 的最值。
的最值。
(1)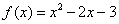 (2)函數(shù)g(x)的單調(diào)遞增區(qū)間為(﹣∞,
(2)函數(shù)g(x)的單調(diào)遞增區(qū)間為(﹣∞, ),(1,+∞).在x2=1有極小值為0.在
),(1,+∞).在x2=1有極小值為0.在 有極大值
有極大值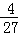 .(3)函數(shù)g(x)的最大值為2,最小值為0.
.(3)函數(shù)g(x)的最大值為2,最小值為0.
解析試題分析:(1)由f(x)=ax2+bx﹣3,知f′(x)=2ax+b.由二次函數(shù)f(x)=ax2+bx﹣3在x=1處取得極值,且在(0,﹣3)點處的切線與直線2x+y=0平行,知 ,由此能求出f(x).
,由此能求出f(x).
(2)由f(x)=x2﹣2x﹣3,知g(x)=xf(x)+4x=x3﹣2x2+x,所以g′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1).令g′(x)=0,得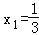 ,x2=1.列表討論能求出函數(shù)g(x)=xf(x)+4x的單調(diào)遞增區(qū)間及極值.
,x2=1.列表討論能求出函數(shù)g(x)=xf(x)+4x的單調(diào)遞增區(qū)間及極值.
(3)由g(0)=0,g(2)=2,結(jié)合(2)的結(jié)論,能求出函數(shù)g(x)的最大值和最小值.
試題解析:(1)由 ,可得
,可得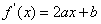 . 由題設(shè)可得
. 由題設(shè)可得 即
即
解得 ,
,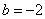 .所以
.所以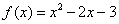 .
.
(2)由題意得 ,所以
,所以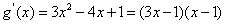 .令
.令 ,得
,得 ,
,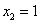 .
.