
���}Ŀ��ijУ���u���½̸Č��̌W(xu��)��Ӱ푣����x��ˮƽ�ஔ(d��ng)?sh��)ăɂ�ƽ�а��M(j��n)�Ќ���ԇ�װ���Ä�(chu��ng)�½̷����Ұ��Բ��Â��y(t��ng)�̷���һ�Εr�g���M(j��n)��ˮƽ�yԇ���ɿ��Y(ji��)��ȫ������![]() �^(q��)�g��(n��i)���M��100�֣������L���l�ʷֲ�ֱ���D���҈D���ɂ����˔�(sh��)����60�ˣ��ɿ�80�ּ����Ϟ郞(y��u)����
�^(q��)�g��(n��i)���M��100�֣������L���l�ʷֲ�ֱ���D���҈D���ɂ����˔�(sh��)����60�ˣ��ɿ�80�ּ����Ϟ郞(y��u)����

����(j��)������Ϣ�������![]() (li��n)�������Д���ж��İ����J(r��n)��W(xu��)���ɿ���(y��u)���c�༉���P(gu��n)��
(li��n)�������Д���ж��İ����J(r��n)��W(xu��)���ɿ���(y��u)���c�༉���P(gu��n)��

��2���༉�ӳ��,��ȡ�ɿ���(y��u)����5�˅�����Մ���F(xi��n)��5�����S�C(j��)�x3�ˁ�������l(f��)�ԣ���l(f��)����������2�ˁ��Լװ�ĸ��ʡ�
(�����R��ֵ����ʽ�H������

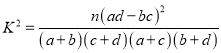 ,
, ![]() )
)
���𰸡���1����90���İ��գ�2��![]()
��������ԇ�}������(1)����(j��)���o��(sh��)��(j��)�ɵ���(li��n)���������Д�(sh��)��(j��)���빫ʽ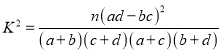 ����
����![]() ��ֵ���c
��ֵ���c![]() ���^���ɵýY(ji��)Փ��(2) �ӳ�Ӽװ��ȡ��3�ˣ�ӛ��
���^���ɵýY(ji��)Փ��(2) �ӳ�Ӽװ��ȡ��3�ˣ�ӛ��![]() ,�Ұ��ȡ��2��,ӛ��
,�Ұ��ȡ��2��,ӛ��![]() �����������ȡ3�˹���
�����������ȡ3�˹���![]() �N�����������}��Ĺ���
�N�����������}��Ĺ���![]() �N���ɹŵ�����ʹ�ʽ�ɵýY(ji��)��.
�N���ɹŵ�����ʹ�ʽ�ɵýY(ji��)��.
ԇ�}����:��1��
�Ƿ� ��(y��u)�� �༉ | ��(y��u)�� ���˔�(sh��)�� | �ǃ�(y��u)�� ���˔�(sh��)�� | ��Ӌ |
�� | 30 | 30 | 60 |
�� | 20 | 40 | 60 |
��Ӌ | 50 | 70 | 120 |
![]()
�t��90���İ����J(r��n)��W(xu��)���ɿ���(y��u)���c�༉���P(gu��n)��
��2���ӳ�Ӽװ��ȡ��3�ˣ�ӛ��![]() ,�Ұ��ȡ��2��,ӛ��
,�Ұ��ȡ��2��,ӛ��![]() �����������ȡ3�ˣ���
�����������ȡ3�ˣ���![]()
![]()
![]()
![]()
![]() 10�N���Σ�����������2�ˁ��Լװ����7�N���Σ�
10�N���Σ�����������2�ˁ��Լװ����7�N���Σ�
�t������2�ˁ��Լװ�ĸ��ʞ�![]() ��
��


 ���б�ˢ�}ϵ�д�
���б�ˢ�}ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() �քe����
�քe����![]() �����c.
�����c.
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2�����C��ƽ��![]()
![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ���돽��R�İ�A��(n��i)���Ӱ������ֱ��AB����ֱ�����S�����D(zhu��n)һ�ܵõ�һ���w����ԓ���w�ı���e�����С�BAC=30�㣩�����w�e�� 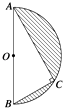
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
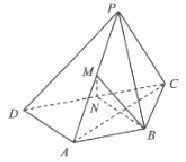
���}Ŀ����D��һ���νM���w�������ABCD�������Σ���PD�cEC����ֱ�ڵ���ABCD��PD=2EC��N��PB�����c�����C�� 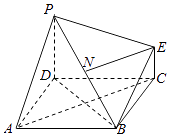
��1��ƽ��EBC��ƽ��PDA��
��2��NE��ƽ��PDB��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������FP��ABCD�У���(c��)��PCD�͵���ABCD��PD��CD��E��PC���c������ABCD��ֱ�����Σ�AB��CD����ADC=90�㣬AB=AD=PD=1��CD=2��
�������C��BE��ƽ��APD��
�������C��BC��ƽ��PBD��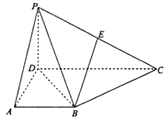
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڡ�ABC�У�a=2��A=45�㣬�����������Ѓɽ⣬�tb��ȡֵ�����ǣ� ��
A.��2��2 ![]() ��
��
B.��2��+�ޣ�
C.�����ޣ�2��
D.�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��������ABCD�У�BC��AD��AB��BC��AB=BC=1��PA=AD=2��PA��ƽ��ABCD��E��PD���c�� 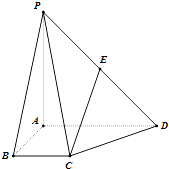
��1�����C��CE��ƽ��PAB��
��2����ֱ��CE�cƽ��PAD���ɽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��A.��D��ʾ, ![]() �Lj@
�Lj@![]() ��(n��i)�ɗl��
��(n��i)�ɗl��![]() ��
��![]() �Ľ��c,�^
�Ľ��c,�^![]() ���L����һ�c
���L����һ�c![]() ���A
���A![]() ���о�
���о�![]() ,
, ![]() �����c,��֪
�����c,��֪![]() ���C:
���C: ![]()

B.��֪���![]()
![]() ,
, ![]()
![]() .����
.����![]() ,ʹ��
,ʹ��![]()
C.��ƽ��ֱ������(bi��o)ϵ![]() ��,ֱ��
��,ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞� (
(![]() �酢��(sh��)),������(bi��o)ԭ�c
�酢��(sh��)),������(bi��o)ԭ�c![]() ��O�c,
��O�c, ![]() �S�����S��O�S�ĘO����(bi��o)ϵ��,����
�S�����S��O�S�ĘO����(bi��o)ϵ��,����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ,��ֱ֪��
,��ֱ֪��![]() �c����
�c����![]() �ཻ��
�ཻ��![]() ���c,��
���c,��![]() ���L.
���L.
D.��֪![]() ��������(sh��),��
��������(sh��),��![]() ,���C:
,���C: ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪һ�A��(j��ng)�^�cA��2����3����B����2����5�����҈A��C��ֱ��l��x��2y��3=0�ϣ���ˈA�ķ��̣�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com