
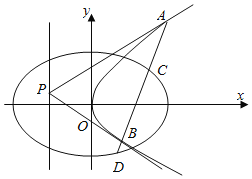
【題目】若給定橢圓![]() 和點
和點![]() ,則稱直線
,則稱直線![]() 為橢圓C的“伴隨直線”.
為橢圓C的“伴隨直線”.
(1)若![]() 在橢圓C上,判斷橢圓C與它的“伴隨直線”的位置關(guān)系(當(dāng)直線與橢圓的交點個數(shù)為0個、1個、2個時,分別稱直線與橢圓相離、相切、相交),并說明理由;
在橢圓C上,判斷橢圓C與它的“伴隨直線”的位置關(guān)系(當(dāng)直線與橢圓的交點個數(shù)為0個、1個、2個時,分別稱直線與橢圓相離、相切、相交),并說明理由;
(2)命題:“若點![]() 在橢圓C的外部,則直線
在橢圓C的外部,則直線![]() 與橢圓C必相交.”寫出這個命題的逆命題,判斷此逆命題的真假,說明理由;
與橢圓C必相交.”寫出這個命題的逆命題,判斷此逆命題的真假,說明理由;
(3)若![]() 在橢圓C的內(nèi)部,過N點任意作一條直線,交橢圓C于A、B,交
在橢圓C的內(nèi)部,過N點任意作一條直線,交橢圓C于A、B,交![]() 于M點(異于A、B),設(shè)
于M點(異于A、B),設(shè)![]() ,問
,問![]() 是否為定值?說明理由.
是否為定值?說明理由.
【答案】(1)l與橢圓C相切.見解析(2)逆命題:若直線![]() 與橢圓C相交,則點
與橢圓C相交,則點![]() 在橢圓C的外部.是真命題.見解析(3)為定值0,見解析
在橢圓C的外部.是真命題.見解析(3)為定值0,見解析
【解析】
(1) 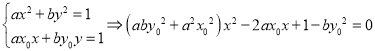 ,由根的差別式能得到l與橢圓C相切.
,由根的差別式能得到l與橢圓C相切.
(2)逆命題:若直線![]() 與橢圓C相交,則點
與橢圓C相交,則點![]() 在橢圓C的外部.是真命題.聯(lián)立方程得
在橢圓C的外部.是真命題.聯(lián)立方程得![]() .由
.由![]() ,能求出
,能求出![]() 在橢圓C的外部.
在橢圓C的外部.
(3)此時![]() 與橢圓相離,設(shè)
與橢圓相離,設(shè)![]() 則
則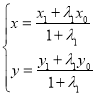 代入橢圓
代入橢圓![]() ,利用M在
,利用M在![]() 上,得
上,得![]() .由此能求出
.由此能求出![]() .
.
解:(1)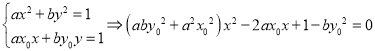
即![]()
∴![]()
∴![]() 與橢圓C相切.
與橢圓C相切.
(2)逆命題:若直線![]() 與橢圓C相交,
與橢圓C相交,
則點![]() 在橢圓C的外部.
在橢圓C的外部.
是真命題.聯(lián)立方程得![]()
則![]()
∴![]()
∴![]()
∴![]() 在橢圓C的外部.
在橢圓C的外部.
(3)同理可得此時![]() 與橢圓相離,設(shè)
與橢圓相離,設(shè)![]()
則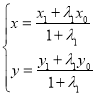 代入橢圓
代入橢圓![]() ,利用M在
,利用M在![]() 上,
上,
即![]() ,整理得
,整理得![]()
同理得關(guān)于![]() 的方程,類似.
的方程,類似.
即![]() 是
是![]() 的兩根
的兩根
∴![]() .
.


 名校名師培優(yōu)作業(yè)本加核心試卷系列答案
名校名師培優(yōu)作業(yè)本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是各項均為非零實數(shù)的數(shù)列
是各項均為非零實數(shù)的數(shù)列![]() 的前n項和,給出如下兩個命題上:命題p:
的前n項和,給出如下兩個命題上:命題p:![]() 是等差數(shù)列;命題q:等式
是等差數(shù)列;命題q:等式![]() 對任意
對任意![]()
![]() 恒成立,其中k,b是常數(shù).
恒成立,其中k,b是常數(shù).
(1)若p是q的充分條件,求k,b的值;
(2)對于(1)中的k與b,問p是否為q的必要條件,請說明理由;
(3)若p為真命題,對于給定的正整數(shù)n![]() 和正數(shù)M,數(shù)列
和正數(shù)M,數(shù)列![]() 滿足條件
滿足條件![]() ,試求
,試求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的長軸是短軸的兩倍,以短軸一個頂點和長軸一個頂點為端點的線段作直徑的圓的周長等于
的長軸是短軸的兩倍,以短軸一個頂點和長軸一個頂點為端點的線段作直徑的圓的周長等于![]() ,直線l與橢圓C交于
,直線l與橢圓C交于![]() 兩點,其中直線l不過原點.
兩點,其中直線l不過原點.
(1)求橢圓C的方程;
(2)設(shè)直線![]() 的斜率分別為
的斜率分別為![]() ,其中
,其中![]() 且
且![]() .記
.記![]() 的面積為S.分別以
的面積為S.分別以![]() 為直徑的圓的面積依次為
為直徑的圓的面積依次為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校為調(diào)查學(xué)生喜歡“應(yīng)用統(tǒng)計”課程是否與性別有關(guān),隨機(jī)抽取了選修課程的55名學(xué)生,得到數(shù)據(jù)如下表:
喜歡統(tǒng)計課程 | 不喜歡統(tǒng)計課程 | ||
男生 | 20 | 5 | |
女生 | 10 | 20 | |
(1)判斷是否有99.5%的把握認(rèn)為喜歡“應(yīng)用統(tǒng)計”課程與性別有關(guān)?
(2)用分層抽樣的方法從喜歡統(tǒng)計課程的學(xué)生中抽取6名學(xué)生作進(jìn)一步調(diào)查,將這6名學(xué)生作為一個樣本,從中任選2人,求恰有1個男生和1個女生的概率.
臨界值參考:
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知中心在原點的橢圓![]() 和拋物線
和拋物線![]() 有相同的焦點
有相同的焦點![]() ,橢圓
,橢圓![]() 過點
過點![]() ,拋物線
,拋物線![]() 的頂點為原點.
的頂點為原點.
![]() 求橢圓
求橢圓![]() 和拋物線
和拋物線![]() 的方程;
的方程;
![]() 設(shè)點P為拋物線
設(shè)點P為拋物線![]() 準(zhǔn)線上的任意一點,過點P作拋物線
準(zhǔn)線上的任意一點,過點P作拋物線![]() 的兩條切線PA,PB,其中A,B為切點.
的兩條切線PA,PB,其中A,B為切點.
![]() 設(shè)直線PA,PB的斜率分別為
設(shè)直線PA,PB的斜率分別為![]() ,
,![]() ,求證:
,求證:![]() 為定值;
為定值;
![]() 若直線AB交橢圓
若直線AB交橢圓![]() 于C,D兩點,
于C,D兩點,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的面積,試問:
的面積,試問:![]() 是否有最小值?若有,求出最小值;若沒有,請說明理由.
是否有最小值?若有,求出最小值;若沒有,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 焦點為
焦點為![]() ,
,![]() 為拋物線上在第一象限內(nèi)一點,
為拋物線上在第一象限內(nèi)一點,![]() 為原點,
為原點,![]() 面積為
面積為![]() .
.
(1)求拋物線方程;
(2)過![]() 點作兩條直線分別交拋物線于異于點
點作兩條直線分別交拋物線于異于點![]() 的兩點
的兩點![]() ,
,![]() ,且兩直線斜率之和為
,且兩直線斜率之和為![]() ,
,
(i)若![]() 為常數(shù),求證直線
為常數(shù),求證直線![]() 過定點
過定點![]() ;
;
(ii)當(dāng)![]() 改變時,求(i)中距離
改變時,求(i)中距離![]() 最近的點
最近的點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2022年北京冬奧會的申辦成功與“3億人上冰雪”口號的提出,將冰雪這個冷項目迅速炒“熱”.北京某綜合大學(xué)計劃在一年級開設(shè)冰球課程,為了解學(xué)生對冰球運(yùn)動的興趣,隨機(jī)從該校一年級學(xué)生中抽取了100人進(jìn)行調(diào)查,其中女生中對冰球運(yùn)動有興趣的占![]() ,而男生有10人表示對冰球運(yùn)動沒有興趣額.
,而男生有10人表示對冰球運(yùn)動沒有興趣額.
(1)完成![]() 列聯(lián)表,并回答能否有
列聯(lián)表,并回答能否有![]() 的把握認(rèn)為“對冰球是否有興趣與性別有關(guān)”?
的把握認(rèn)為“對冰球是否有興趣與性別有關(guān)”?
有興趣 | 沒興趣 | 合計 | |
男 | 55 | ||
女 | |||
合計 |
(2)已知在被調(diào)查的女生中有5名數(shù)學(xué)系的學(xué)生,其中3名對冰球有興趣,現(xiàn)在從這5名學(xué)生中隨機(jī)抽取3人,求至少有2人對冰球有興趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)的甲、乙、丙三名同學(xué)參加高校自主招生考試,每位同學(xué)彼此獨(dú)立的從![]() 四所高校中選2所.
四所高校中選2所.
(Ⅰ)求甲、乙、丙三名同學(xué)都選![]() 高校的概率;
高校的概率;
(Ⅱ)若已知甲同學(xué)特別喜歡![]() 高校,他必選
高校,他必選![]() 校,另在
校,另在![]() 三校中再隨機(jī)選1所;而同學(xué)乙和丙對四所高校沒有偏愛,因此他們每人在四所高校中隨機(jī)選2所.
三校中再隨機(jī)選1所;而同學(xué)乙和丙對四所高校沒有偏愛,因此他們每人在四所高校中隨機(jī)選2所.
(ⅰ)求甲同學(xué)選![]() 高校且乙、丙都未選
高校且乙、丙都未選![]() 高校的概率;
高校的概率;
(ⅱ)記![]() 為甲、乙、丙三名同學(xué)中選
為甲、乙、丙三名同學(xué)中選![]() 校的人數(shù),求隨機(jī)變量
校的人數(shù),求隨機(jī)變量![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() .
.
(Ⅰ)求橢圓![]() 的方程,并求其離心率;
的方程,并求其離心率;
(Ⅱ)過點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,設(shè)點
,設(shè)點![]() 為第四象限內(nèi)一點且在橢圓
為第四象限內(nèi)一點且在橢圓![]() 上(點
上(點![]() 不在直線
不在直線![]() 上),直線
上),直線![]() 關(guān)于
關(guān)于![]() 的對稱直線
的對稱直線![]() 與橢圓交于另一點
與橢圓交于另一點![]() .設(shè)
.設(shè)![]() 為坐標(biāo)原點,判斷直線
為坐標(biāo)原點,判斷直線![]() 與直線
與直線![]() 的位置關(guān)系,并說明理由.
的位置關(guān)系,并說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com