
【題目】已知函數(shù) ![]() 的定義域?yàn)榧螦,y=﹣x2+2x+2a的值域?yàn)锽.
的定義域?yàn)榧螦,y=﹣x2+2x+2a的值域?yàn)锽.
(1)若a=2,求A∩B
(2)若A∪B=R,求實(shí)數(shù)a的取值范圍.
【答案】
(1)解:依題意:整理得A={x︳x>3},函數(shù)y=﹣x2+2x+2a=﹣(x﹣1)2+1+2a≤1+2a,即B={x︳x≤2a+1},
當(dāng)a=2時(shí),B={x|x≤5},
∴A∩B={x︳3<x≤5}
(2)解:∵A∪B=R,∴根據(jù)題意得:2a+1≥3,
解得:a≥1,
則實(shí)數(shù)a的取值范圍是[1,+∞)
【解析】求出函數(shù)y= ![]() 的定義域確定出A,求出y=﹣x2+2x+2a的值域確定出B,(1)把a(bǔ)=2代入確定出B,求出A與B的交集即可;(2)由A與B的并集為R,列出關(guān)于a的不等式,求出不等式的解集即可得到a的范圍.
的定義域確定出A,求出y=﹣x2+2x+2a的值域確定出B,(1)把a(bǔ)=2代入確定出B,求出A與B的交集即可;(2)由A與B的并集為R,列出關(guān)于a的不等式,求出不等式的解集即可得到a的范圍.
【考點(diǎn)精析】根據(jù)題目的已知條件,利用集合的并集運(yùn)算和集合的交集運(yùn)算的相關(guān)知識(shí)可以得到問題的答案,需要掌握并集的性質(zhì):(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,則A
=A,A∪B=B∪A;(2)若A∪B=B,則A![]() B,反之也成立;交集的性質(zhì):(1)A∩B
B,反之也成立;交集的性質(zhì):(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,則A
,A∩B=B∩A;(2)若A∩B=A,則A![]() B,反之也成立.
B,反之也成立.


 名師指導(dǎo)期末沖刺卷系列答案
名師指導(dǎo)期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)生產(chǎn)的新產(chǎn)品必須先靠廣告打開銷路,該產(chǎn)品廣告效應(yīng)y(單位:元)是產(chǎn)品的銷售額與廣告費(fèi)x(單位:元)之間的差,如果銷售額與廣告費(fèi)x的算術(shù)平方根成正比,根據(jù)對(duì)市場(chǎng)的抽樣調(diào)查,每付出100元的廣告費(fèi),所得銷售額是1000元. (Ⅰ)求出廣告效應(yīng)y與廣告費(fèi)x之間的函數(shù)關(guān)系式;
(Ⅱ)該企業(yè)投入多少廣告費(fèi)才能獲得最大的廣告效應(yīng)?是不是廣告費(fèi)投入越多越好?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,側(cè)棱
中,側(cè)棱![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn)
的中點(diǎn)
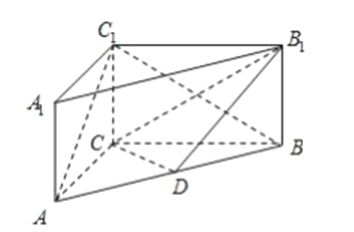
(1)證明: ![]() 平面
平面![]() ;
;
(2)在線段![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使得直線
,使得直線![]() 與
與![]() 所成角的為
所成角的為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】共享單車是指由企業(yè)在校園、公交站點(diǎn)、商業(yè)區(qū)、公共服務(wù)區(qū)等場(chǎng)所提供的自行車單車共享服務(wù),由于其依托“互聯(lián)網(wǎng)+”,符合“低碳出行”的理念,已越來越多地引起了人們的關(guān)注.某部門為了對(duì)該城市共享單車加強(qiáng)監(jiān)管,隨機(jī)選取了100人就該城市共享單車的推行情況進(jìn)行問卷調(diào)查,并將問卷中的這100人根據(jù)其滿意度評(píng)分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5組,制成如圖所示頻率分直方圖.
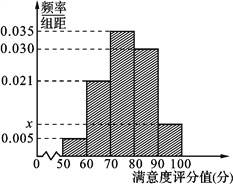
(1) 求圖中![]() 的值;
的值;
(2) 已知滿意度評(píng)分值在[90,100]內(nèi)的男生數(shù)與女生數(shù)的比為2:1,若在滿意度評(píng)分值為[90,100]的人中隨機(jī)抽取4人進(jìn)行座談,設(shè)其中的女生人數(shù)為隨機(jī)變量![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)是定義在區(qū)間(0,+∞)上的增函數(shù),f(2)=1,且對(duì)于任意a,b∈(0,+∞), ![]() 恒成立. (I)求f(8);
恒成立. (I)求f(8);
(II)求不等式 ![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】矩形![]() 中,
中, ![]() ,
, ![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 中點(diǎn),沿
中點(diǎn),沿![]() 將
將![]() 折起至
折起至![]() ,如下圖所示,點(diǎn)
,如下圖所示,點(diǎn)![]() 在面
在面![]() 的射影
的射影![]() 落在
落在![]() 上.
上.
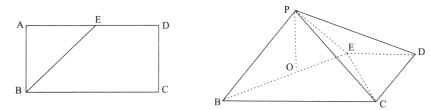
(Ⅰ)求證: ![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為評(píng)估設(shè)備![]() 生產(chǎn)某種零件的性能,從設(shè)備
生產(chǎn)某種零件的性能,從設(shè)備![]() 生產(chǎn)零件的流水線上隨機(jī)抽取100件零件作為樣本,測(cè)量其直徑后,整理得到下表:
生產(chǎn)零件的流水線上隨機(jī)抽取100件零件作為樣本,測(cè)量其直徑后,整理得到下表:
直徑/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計(jì) |
件數(shù) | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經(jīng)計(jì)算,樣本的平均值![]() ,標(biāo)準(zhǔn)差
,標(biāo)準(zhǔn)差![]() ,以頻率值作為概率的估計(jì)值.
,以頻率值作為概率的估計(jì)值.
(1)為評(píng)判一臺(tái)設(shè)備的性能,從該設(shè)備加工的零件中任意抽取一件,記其直徑為![]() ,并根據(jù)以下不等式進(jìn)行評(píng)判(
,并根據(jù)以下不等式進(jìn)行評(píng)判(![]() 表示相應(yīng)事件的概率);
表示相應(yīng)事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
評(píng)判規(guī)則為:若同時(shí)滿足上述三個(gè)不等式,則設(shè)備等級(jí)為甲;僅滿足其中兩個(gè),則等級(jí)為乙;若僅滿足其中一個(gè),則等級(jí)為丙;若全部不滿足,則等級(jí)為丁,試判斷設(shè)備![]() 的性能等級(jí).
的性能等級(jí).
(2)將直徑小于等于![]() 或直徑大于
或直徑大于![]() 的零件認(rèn)為是次品.
的零件認(rèn)為是次品.
①從設(shè)備![]() 的生產(chǎn)流水線上隨意抽取2件零件,計(jì)算其中次品個(gè)數(shù)
的生產(chǎn)流水線上隨意抽取2件零件,計(jì)算其中次品個(gè)數(shù)![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望![]() ;
;
②從樣本中隨意抽取2件零件,計(jì)算其中次品個(gè)數(shù)![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)定義在[﹣2,2]上的奇函數(shù)f(x)=x5+x3+b
(1)求b值;
(2)若f(x)在[0,2]上單調(diào)遞增,且f(m)+f(m﹣1)>0,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
, ![]() ,動(dòng)點(diǎn)
,動(dòng)點(diǎn)![]() 滿足
滿足![]() .設(shè)動(dòng)點(diǎn)
.設(shè)動(dòng)點(diǎn)![]() 的軌跡為
的軌跡為![]() .
.
(1)求動(dòng)點(diǎn)![]() 的軌跡方程,并說明軌跡
的軌跡方程,并說明軌跡![]() 是什么圖形;
是什么圖形;
(2)求動(dòng)點(diǎn)![]() 與定點(diǎn)
與定點(diǎn)![]() 連線的斜率的最小值;
連線的斜率的最小值;
(3)設(shè)直線![]() 交軌跡
交軌跡![]() 于
于![]() 兩點(diǎn),是否存在以線段
兩點(diǎn),是否存在以線段![]() 為直徑的圓經(jīng)過
為直徑的圓經(jīng)過![]() ?若存在,求出實(shí)數(shù)
?若存在,求出實(shí)數(shù)![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com