
【題目】已知非零向量 ![]() ,
, ![]() 滿足|
滿足| ![]() |=1,且(
|=1,且( ![]() ﹣
﹣ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() .
.
(1)求| ![]() |;
|;
(2)當 ![]()
![]() =-
=- ![]() 時,求向量
時,求向量 ![]() 與
與 ![]() +2
+2 ![]() 的夾角θ的值.
的夾角θ的值.
【答案】
(1)解:因為( ![]() ﹣
﹣ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() ,即
,即 ![]() =
= ![]() ,即|
,即| ![]() |2﹣|
|2﹣| ![]() |2=
|2= ![]() ,
,
所以,| ![]() |2=|
|2=| ![]() |2﹣
|2﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() ,故|
,故| ![]() |=
|= ![]()
(2)解:因為| ![]() |2 =|
|2 =| ![]() |2+4
|2+4 ![]() +|2
+|2 ![]() |2=1﹣1+1=1,故|
|2=1﹣1+1=1,故| ![]() |=1.
|=1.
又因為 ![]() (
( ![]() )=|
)=| ![]() |2+2
|2+2 ![]() =1﹣
=1﹣ ![]() =
= ![]() ,
,
∴cos θ= 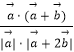 ═
═ ![]() ,
,
又0°≤θ≤180°,故θ=60°
【解析】(1)由( ![]() ﹣
﹣ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() 可得
可得 ![]() =
= ![]() ,再由|
,再由| ![]() |=1求得|
|=1求得| ![]() |2=
|2= ![]() ,從而求得|
,從而求得| ![]() |.(2)由
|.(2)由 ![]()
![]() =-
=- ![]() 求得|
求得| ![]() |=1,再求得
|=1,再求得 ![]() (
( ![]() )=1,利用兩個向量的夾角公式求得cosθ的值,即可求得θ的值.
)=1,利用兩個向量的夾角公式求得cosθ的值,即可求得θ的值.
【考點精析】根據題目的已知條件,利用數量積表示兩個向量的夾角的相關知識可以得到問題的答案,需要掌握設![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 與
與![]() 的夾角,則
的夾角,則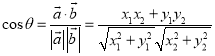 .
.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:
【題目】已知公差不為0的等差數列{an}滿足:a1=1且a2 , a5 , a14成等比數列.
(1)求數列{an}的通項公式an和前n項和Sn;
(2)證明不等式 ![]() 且n∈N*)
且n∈N*)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高一年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
分組 | 頻數 | 頻率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合計 |
| 1 |

(1)求出表中![]() 及圖中
及圖中![]() 的值;
的值;
(2)試估計他們參加社區服務的平均次數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至少1人參加社區服務次數在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+)(A,ω,是常數,A>0,ω>0)的部分圖象如圖所示,下列結論: ①最小正周期為π;
②將f(x)的圖象向左平移 ![]() 個單位,所得到的函數是偶函數;
個單位,所得到的函數是偶函數;
③f(0)=1;
④ ![]() ;
;
⑤ ![]() .
.
其中正確的是( )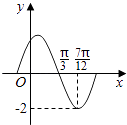
A.①②③
B.②③④
C.①④⑤
D.②③⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在坐標原點,焦點在x軸上,橢圓C上的點到焦點距離的最大值為3,離心率 ![]() .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)若經過左焦點F1且傾斜角為 ![]() 的直線l與橢圓交于A、B兩點,求|AB|的值.
的直線l與橢圓交于A、B兩點,求|AB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的二次函數f(x)=ax2﹣4bx+1
(Ⅰ)設集合P={1,2,3},集合Q={﹣1,1,2,3,4},從集合P中隨機取一個數作為a,從集合Q中隨機取一個數作為b,求函數f(x)在區間[1,+∞)上是增函數的概率;
(Ⅱ)設點(a,b)是區域 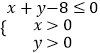 內的隨機點,求函數f(x)在區間[1,+∞)上是增函數的概率.
內的隨機點,求函數f(x)在區間[1,+∞)上是增函數的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C的方程為x2+y2﹣8x+15=0,若直線y=kx﹣2上至少存在一點,使得以該點為圓心,1為半徑的圓與圓C有公共點,則k的最大值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為 ![]() ,且a1與a5的等差中項為18.
,且a1與a5的等差中項為18.
(1)求{an}的通項公式;
(2)若an=2log2bn , 求數列{bn}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com