【題目】若三棱錐
的四個面都為直角三角形,
平面
,
,
,則三棱錐中最長的棱長為( )
A.
B.
C.
D.
【答案】B
【解析】
根據題意，畫出滿足題意的三棱錐，求解棱長即可.
因為
平面
，故
，且
，
則
為直角三角形，由
以及勾股定理得：
；
同理，因為則
為直角三角形，由
，
以及勾股定理得：
；
在保證和均為直角三角形的情況下，
①若
，則在
中，由勾股定理得：
，
此時在
中，由
，
及
，
不滿足勾股定理
故當時，無法保證為直角三角形.
不滿足題意.
②若
，則
，
又因為
面ABC，
面ABC，則
，
故
面PAB，又
面PAB，故
，
則此時可以保證也為直角三角形.滿足題意.
③若
，在直角三角形BCA中，
斜邊AB=2，小于直角邊AC=
，顯然不成立.
綜上所述：當且僅當時，可以保證四棱錐
的四個面均為直角三角形，故作圖如下：
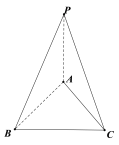
由已知和勾股定理可得：
，
顯然，最長的棱為
.
故選：B.
科目：高中數學 來源： 題型：
【題目】如圖，在正方體
中，
是
的中點.
（1）求證：
平面
；
（2）求證：平面
平面.（只需在下面橫線上填寫給出的如下結論的序號：①
平面
，②
平面，③
，④
，⑤
）
證明：（1）設
，連接
.因為底面
是正方形，所以
為
的中點，又是的中點，所以_________.因為
平面，____________，所以平面.
（2）因為
平面
平面，所以___________，因為底面是正方形，所以_______，又因為
平面
平面，所以_________.又
平面，所以平面平面.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示，其中成績分組區(qū)間是：[50,60][60,70][70,80][80,90][90,100].
(1)求圖中a的值；
(2)根據頻率分布直方圖，估計這100名學生語文成績的平均分；
(3)若這100名學生語文成績某些分數段的人數（x）與數學成績相應分數段的人數（y）之比如下表所示，求數學成績在[50，90）之外的人數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某同學用“五點法”畫函數
在某一個周期內的圖象時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)請將上表數據補充完整,填寫在相應位置,并求出函數
的解析式;
(2)把
的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再把得到的圖象向左平移
個單位長度,得到函數
的圖象,求
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
