Question

【題目】已知， .

（1）求函數(shù)的最小值；

（2）對一切， 恒成立，求實數(shù)的取值范圍.

Answer 1

【答案】(1) ;(2) .

【解析】試題分析：（1）求出，利用導(dǎo)數(shù)與單調(diào)性的關(guān)系，分類求解；（2））由已知， ，分離參數(shù)，則，構(gòu)造 (x＞0) 通過研究h（x）的最值確定a的范圍．

試題解析：解：（1），

當(dāng)， ，f(x)單調(diào)遞減，當(dāng)， ，f(x)單調(diào)遞增

①，沒有最小值；

②，即時， ；

③，即時，f（x）在[t，t+2]上單調(diào)遞增， ；

所以;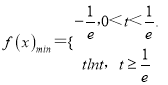

（2）由已知， ，則，

設(shè)，則，

①x∈（0，1），h'（x）＜0，h（x）單調(diào)遞減，

②x∈（1，+∞），h'（x）＞0，h（x）單調(diào)遞增，

所以h（x）min=h（1）=4，對一切x∈（0，+∞），2f（x）≥g（x）恒成立，

所以a≤h（x）min=4；，所以a的范圍是（-∞，4].