
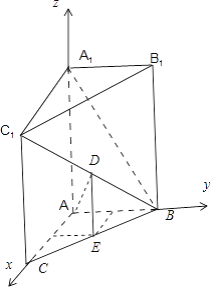
【題目】如圖,在三棱柱ABC﹣A1B1C1中,AA1C1C是邊長為4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(Ⅰ)求證:AA1⊥平面ABC;
(Ⅱ)求證二面角A1﹣BC1﹣B1的余弦值;
【答案】(Ⅰ)見解析;(Ⅱ) ![]() .
.
【解析】試題分析:(Ⅰ)先利用正方形得到線線垂直,再利用面面垂直的性質定理進行證明;(Ⅱ)利用勾股定理證明線線垂直,合理建立空間直角坐標系,寫出出相關點的坐標,求出相關平面的法向量,再通過空間向量的夾角公式進行求解.
試題解析:(I)證明:∵AA1C1C是正方形,∴AA1⊥AC.又∵平面ABC⊥平面AA1C1C,平面ABC∩平面AA1C1C=AC,
∴AA1⊥平面ABC.
(II)由AC=4,BC=5,AB=3.
∴AC2+AB2=BC2,∴AB⊥AC.
建立如圖所示的空間直角坐標系,則A1(0,0,4),B(0,3,0),B1(0,3,4),C1(4,0,4),∴![]() ,
,![]() ,
,![]() .
.
設平面A1BC1的法向量為![]() ,平面B1BC1的法向量為
,平面B1BC1的法向量為![]() =
=![]() .
.
則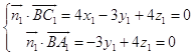 ,令
,令![]() ,解得
,解得![]() ,∴
,∴![]() .
.
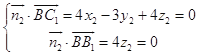 ,令
,令![]() ,解得
,解得![]() ,∴
,∴![]() .
.
![]() =
=![]() =
=![]() =
=![]() .
.
∴二面角A1﹣BC1﹣B1的余弦值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】共享汽車的出現為我們的出行帶來了極大的便利,當然也為投資商帶來了豐厚的利潤。現某公司瞄準這一市場,準備投放共享汽車。該公司取得了在![]() 個省份投放共享汽車的經營權,計劃前期一次性投入
個省份投放共享汽車的經營權,計劃前期一次性投入![]() 元. 設在每個省投放共享汽車的市的數量相同(假設每個省的市的數量足夠多),每個市都投放
元. 設在每個省投放共享汽車的市的數量相同(假設每個省的市的數量足夠多),每個市都投放![]() 輛共享汽車.由于各個市的多種因素的差異,在第
輛共享汽車.由于各個市的多種因素的差異,在第![]() 個市的每輛共享汽車的管理成本為(
個市的每輛共享汽車的管理成本為(![]() )元(其中
)元(其中![]() 為常數).經測算,若每個省在
為常數).經測算,若每個省在![]() 個市投放共享汽車,則該公司每輛共享汽車的平均綜合管理費用為
個市投放共享汽車,則該公司每輛共享汽車的平均綜合管理費用為![]() 元.(本題中不考慮共享汽車本身的費用)
元.(本題中不考慮共享汽車本身的費用)
注:綜合管理費用=前期一次性投入的費用+所有共享汽車的管理費用,平均綜合管理費用=綜合管理費用÷共享汽車總數.
(1)求![]() 的值;
的值;
(2)問要使該公司每輛共享汽車的平均綜合管理費用最低,則每個省有幾個市投放共享汽車?此時每輛共享汽車的平均綜合管理費用為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一臺風中心在港口南偏東![]() 方向上,距離港口
方向上,距離港口![]() 千米處的海面上形成,并以每小時
千米處的海面上形成,并以每小時![]() 千米的速度向正北方向移動,距臺風中心
千米的速度向正北方向移動,距臺風中心![]() 千米以內的范圍將受到臺風的影響,則港口受到臺風影響的時間為( )
千米以內的范圍將受到臺風的影響,則港口受到臺風影響的時間為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某氣象儀器研究所按以下方案測試一種“彈射型”氣象觀測儀器的垂直彈射高度:A、B、C三地位于同一水平面上,在C處進行該儀器的垂直彈射,觀測點A、B兩地相距100米,∠BAC=60°,在A地聽到彈射聲音的時間比在B地晚![]()
秒. A地測得該儀器彈至最高點H時的仰角為30°.
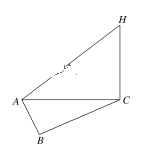
(1)求A、C兩地的距離;
(2)求該儀器的垂直彈射高度CH.(聲音的傳播速度為340米/秒)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐V-ABC中,平面VAB![]() 平面ABC,
平面ABC, ![]() VAB為等邊三角形,AC
VAB為等邊三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分別為AB,VA的中點。
,O,M分別為AB,VA的中點。
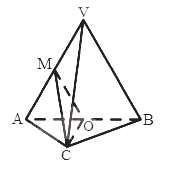
(I)求證:VB//平面MOC;
(II)求證:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱錐V-ABC的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,圓心為
,圓心為![]() ,定點
,定點![]() ,
, ![]() 為圓
為圓![]() 上一點,線段
上一點,線段![]() 上一點
上一點![]() 滿足
滿足![]() ,直線
,直線![]() 上一點
上一點![]() ,滿足
,滿足![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)![]() 為坐標原點,
為坐標原點, ![]() 是以
是以![]() 為直徑的圓,直線
為直徑的圓,直線![]() 與
與![]() 相切,并與軌跡
相切,并與軌跡![]() 交于不同的兩點
交于不同的兩點![]() .當
.當![]() 且滿足
且滿足![]() 時,求
時,求![]() 面積
面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com