(本小題滿分12分)
如圖,在直三棱柱
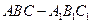
中,
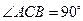
,
是棱
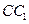
上的動點,
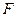
是
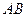
中點,
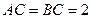
,
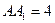
.
(Ⅰ)求證:
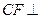
平面
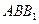
;
(Ⅱ)若二面角
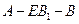
的大小是
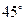
,求
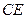
的長.
(Ⅰ)證明見解析
(Ⅱ)

(Ⅰ)證明:∵三棱柱
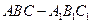
是直棱柱,
∴
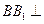
平面
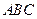
.
又∵

平面
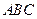
,∴


.
∵
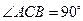
,

,
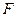
是
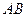
中點,
∴

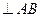
.
又∵
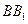
∩

,∴
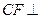
平面
.
(Ⅱ)解:以

為坐標原點,射線

為

軸正半軸,
建立如圖所示的空間直角坐標系
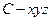
,
則

,
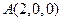
,

.
設(shè)
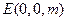
,平面
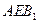
的法向量

,
則

,
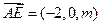
.
且
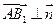
,

.
于是

所以

取
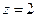
,則

∵三棱柱
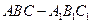
是直棱柱,
∴
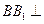
平面
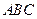
.又∵

平面
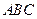
,
∴
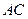

.∵
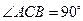
,
∴
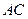

.∵
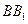
∩

,
∴
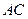

平面

.
∴

是平面

的法向量,

.
∵二面角
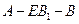
的大小是
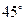
,
∴

.
解得

.∴

.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,在長方體ABCD-A
1B
1C
1D
1中,E,H分別是棱A
1B
1,D
1C
1上的點(點E與B
1不重合),且EH∥A
1 D
1. 過EH的平面與棱BB
1,CC
1相交,交點分別為F,G。
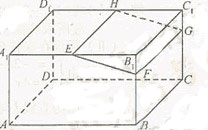
(I) 證明:AD∥平面EFGH;
(II) 設(shè)AB=2AA
1 ="2" a .在長方體ABCD-A
1B
1C
1D
1內(nèi)隨機選取一點。記該點取自幾何體A
1ABFE-D
1DCGH內(nèi)的概率為p,當點E,F(xiàn)分別在棱A
1B
1上運動且滿足EF=a時,求p的最小值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,四棱錐
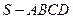
的底面是矩形,
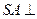
底面
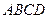
,
P為
BC邊的中點,
SB與
平面
ABCD所成的角為45°,且
AD=2,
SA=1.
(1)求證:
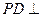
平面
SAP;
(2)求二面角
A-
SD-
P的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
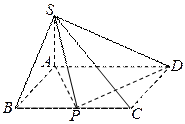
在三棱錐
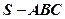
中,
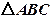
是邊長為
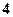
的正三角形,平面
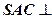
平面
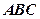
,
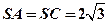
,
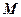
、
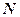
分別為
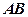
、
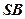
的中點,
(1)證明:
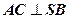
;
(2)求二面角
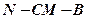
的大小;
(3)求點
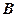
到平面
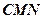
的距離.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
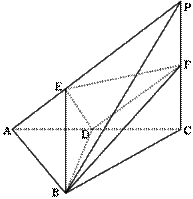
(本小題滿分12分)已知三棱錐P—ABC中,PC⊥底面ABC,
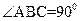
,
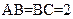
,二面角P-AB-C為
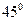
,D、F分別為AC、PC的中點,DE⊥AP于E.
(Ⅰ)求證:AP⊥平面BDE;
(Ⅱ)求平面BEF與平面BAC所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
四面體ABCD中,共頂點A的三條棱兩兩相互垂直,且其長分別為
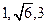
,若四面體的四個頂點同在一個球面上,則這個球的表面積為 。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知兩條不同的直線
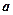
、
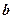
及平面
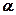
,給出四個下列命題:
(1)若

,
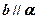
,則
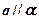
;
(2)若
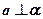
,
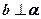
,則

;
(3)若
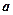
、
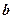
與
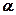
所成的角相等,則

;
(4)若
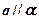
,
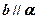
,則

.
其中正確的命題有( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知二面角
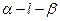
的大小為
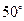
,
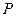
為空間中任意一點,則過點
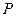
且與平面
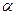
和平面
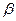
所成的角都是

的直線的條數(shù)為( )
A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
正方體
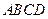
--
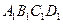
,E、F分別是
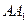
、
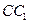
的中點,p是
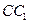
上的動點(包括端點),過E、D、P作正方體的截面,若截面為四邊形,則P的軌跡是
A.線段
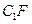
B、線段
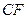
C、線段
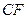
和一點
D、線段
和一點C。
查看答案和解析>>

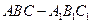 中,
中,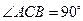 ,
,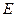 是棱
是棱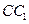 上的動點,
上的動點,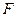 是
是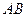 中點,
中點,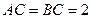 ,
,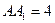 .
.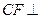 平面
平面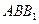 ;
;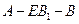 的大小是
的大小是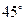 ,求
,求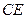 的長.
的長.

 如圖,四棱錐
如圖,四棱錐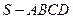 的底面是矩形,
的底面是矩形,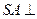 底面
底面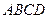 ,P為BC邊的中點,SB與
,P為BC邊的中點,SB與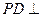 平面SAP;
平面SAP;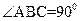 ,
,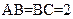 ,二面角P-AB-C為
,二面角P-AB-C為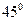 ,D、F分別為AC、PC的中點,DE⊥AP于E.
,D、F分別為AC、PC的中點,DE⊥AP于E.
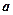 、
、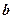 及平面
及平面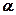 ,給出四個下列命題:
,給出四個下列命題: ,
,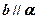 ,則
,則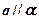 ;
;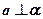 ,
,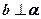 ,則
,則 ;
;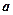 、
、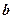 與
與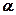 所成的角相等,則
所成的角相等,則 ;
;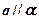 ,
,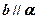 ,則
,則 .
. 個
個 個
個 個
個 個
個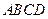 --
--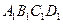 ,E、F分別是
,E、F分別是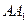 、
、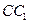 的中點,p是
的中點,p是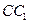 上的動點(包括端點),過E、D、P作正方體的截面,若截面為四邊形,則P的軌跡是
上的動點(包括端點),過E、D、P作正方體的截面,若截面為四邊形,則P的軌跡是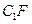 B、線段
B、線段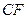 C、線段
C、線段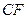 和一點
和一點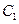 D、線段
D、線段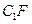 和一點C。
和一點C。