
已知函數(shù)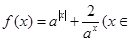 R,
R,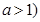 ,
,
(1)求函數(shù)f(x)的值域;
(2)記函數(shù)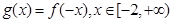 ,若
,若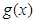 的最小值與
的最小值與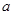 無關(guān),求
無關(guān),求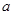 的取值范圍;
的取值范圍;
(3)若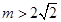 ,直接寫出(不需給出演算步驟)關(guān)于
,直接寫出(不需給出演算步驟)關(guān)于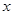 的方程
的方程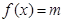 的解集
的解集
(1)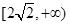 ;(2)
;(2)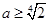 ;(3)①
;(3)①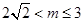 時,解集為
時,解集為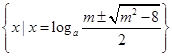 ;
;
②m>3時,解集為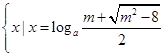 或
或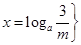
解析試題分析:(1)因解析式中有絕對值,,則把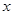 分情況利用基本不等式討論函數(shù)
分情況利用基本不等式討論函數(shù) 的值域;(2)易得函數(shù)
的值域;(2)易得函數(shù)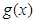 的解析式,再分情況去掉絕對值,利用基本不等求函數(shù)的最小值,從而得結(jié)論;(3)分
的解析式,再分情況去掉絕對值,利用基本不等求函數(shù)的最小值,從而得結(jié)論;(3)分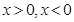 兩種情況求方程的解
兩種情況求方程的解
試題解析:(1)①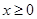 時,
時,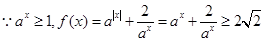 ,
,
當且僅當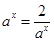 ,即
,即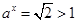 時等號成立;
時等號成立;
②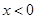 ,
,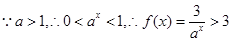 ,由①②知函數(shù)
,由①②知函數(shù) 的值域為
的值域為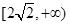
(2) ,
,
①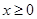 ,
,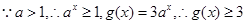 ,
,
②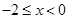 時,
時,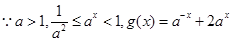 ,
,
令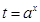 ,則
,則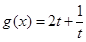 ,記
,記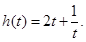
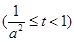 ,
,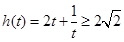 ,當且僅當
,當且僅當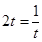 ,
,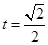 時等號成立,
時等號成立,
(i) ,即
,即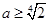 時,結(jié)合①知
時,結(jié)合①知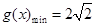 與
與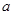 無關(guān);
無關(guān);
(ii)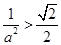 ,即
,即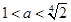 時,
時,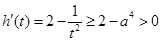 ,
,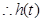 在
在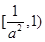 上是增函數(shù),
上是增函數(shù),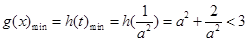 ,
,
結(jié)合①知 與
與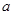 有關(guān);
有關(guān);
綜上,若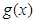 的最小值與
的最小值與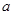 無關(guān),則實數(shù)
無關(guān),則實數(shù)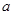 的取值范圍是
的取值范圍是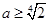
(3)①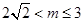 時,關(guān)于
時,關(guān)于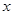 的方程
的方程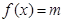 的解集為
的解集為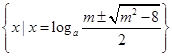 ;
;
②m>3時,關(guān)于x的方程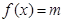 的解集為
的解集為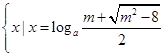 或
或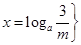
考點:1、利用不等式求函數(shù)的值域;2、利用不等式或?qū)?shù)求最值;3、解指數(shù)方程


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應(yīng)用題卡系列答案
口算與應(yīng)用題卡系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
某市在市內(nèi)主干道北京路一側(cè)修建圓形休閑廣場.如圖,圓形廣場的圓心為O,半徑為100m,并與北京路一邊所在直線 相切于點M.A為上半圓弧上一點,過點A作
相切于點M.A為上半圓弧上一點,過點A作 的垂線,垂足為B.市園林局計劃在△ABM內(nèi)進行綠化.設(shè)△ABM的面積為S(單位:
的垂線,垂足為B.市園林局計劃在△ABM內(nèi)進行綠化.設(shè)△ABM的面積為S(單位: ),
), (單位:弧度).
(單位:弧度).
(I)將S表示為 的函數(shù);
的函數(shù);
(II)當綠化面積S最大時,試確定點A的位置,并求最大面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,
, .
.
(1)若 ,求證:當
,求證:當 時,
時, ;
;
(2)若 在區(qū)間
在區(qū)間 上單調(diào)遞增,試求
上單調(diào)遞增,試求 的取值范圍;
的取值范圍;
(3)求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,點
,點 為一定點,直線
為一定點,直線 分別與函數(shù)
分別與函數(shù) 的圖象和
的圖象和 軸交于點
軸交于點 ,
, ,記
,記 的面積為
的面積為 .
.
(1)當 時,求函數(shù)
時,求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當 時, 若
時, 若 ,使得
,使得 , 求實數(shù)
, 求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)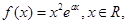 其中
其中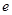 為自然對數(shù)的底數(shù),
為自然對數(shù)的底數(shù), 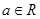 .
.
(1)設(shè)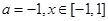 ,求函數(shù)
,求函數(shù)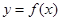 的最值;
的最值;
(2)若對于任意的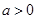 ,都有
,都有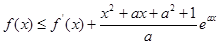 成立,求
成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,
, ,函數(shù)
,函數(shù) 的圖像在點
的圖像在點 處的切線平行于
處的切線平行于 軸.
軸.
(1)求 的值;
的值;
(2)求函數(shù) 的極小值;
的極小值;
(3)設(shè)斜率為 的直線與函數(shù)
的直線與函數(shù) 的圖象交于兩點
的圖象交于兩點 ,(
,( ),證明:
),證明: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
(1)當 時,求函數(shù)
時,求函數(shù) 的極值;
的極值;
(2)若函數(shù) 在定義域內(nèi)為增函數(shù),求實數(shù)m的取值范圍;
在定義域內(nèi)為增函數(shù),求實數(shù)m的取值范圍;
(3)若 ,
, 的三個頂點
的三個頂點 在函數(shù)
在函數(shù) 的圖象上,且
的圖象上,且 ,
, 、
、 、
、 分別為
分別為 的內(nèi)角A、B、C所對的邊。求證:
的內(nèi)角A、B、C所對的邊。求證:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) =
= ,
, =
= ,若曲線
,若曲線 和曲線
和曲線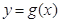 都過點P(0,2),且在點P處有相同的切線
都過點P(0,2),且在點P處有相同的切線 .
.
(Ⅰ)求 ,
, ,
, ,
, 的值;
的值;
(Ⅱ)若 時,
時, ≤
≤ ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com