
【題目】某校高二文科分四個班,各班人數恰好成等差數列,高二數學調研測試后,對四個文科班的學生試卷按每班人數進行分層抽樣,對測試成績進行統計,人數最少的班抽取了![]() 人,抽取的所有學生成績分為
人,抽取的所有學生成績分為![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如圖所示的頻率分布直方圖,其中第六組分數段的人數為
,得到如圖所示的頻率分布直方圖,其中第六組分數段的人數為![]() 人.
人.
(![]() )求
)求![]() 的值,并求出各班抽取的學生數各為多少人?
的值,并求出各班抽取的學生數各為多少人?
(![]() )在抽取的學生中,任取一名學生,求分數不小于
)在抽取的學生中,任取一名學生,求分數不小于![]() 分的概率(視頻率為概率).
分的概率(視頻率為概率).
(![]() )估計高二文科四個班數學成績的平均分
)估計高二文科四個班數學成績的平均分

【答案】(1)各班被抽取的學生人數分別是![]() 人,
人,![]() 人,
人,![]() 人,
人,![]() 人.
人.
(2)![]() .
.
(3)98.
【解析】分析:(1)根據所有頻率和為1可得![]() ,根據題意得到學生總數,再根據等差數列的有關知識求解.(2)由頻率分布直方圖可得所求概率.(3)求出每個小組的中點值和該組頻率乘積的和即可得到成績的平均值.
,根據題意得到學生總數,再根據等差數列的有關知識求解.(2)由頻率分布直方圖可得所求概率.(3)求出每個小組的中點值和該組頻率乘積的和即可得到成績的平均值.
詳解:(![]() )由題意得
)由題意得
![]() ,
,
解得![]() .
.
∵第六組分數段的人數為![]() 人,
人,
∴抽取的學生總數為![]() 人.
人.
∵各班被抽取的學生人數成等差數列,設其公差為![]() ,
,
則由題意得![]() ,
,
解得![]() .
.
∴各班被抽取的學生人數分別是![]() 人,
人,![]() 人,
人,![]() 人,
人,![]() 人.
人.

(![]() )在抽取的學生中,任取一名學生,則分數大小于
)在抽取的學生中,任取一名學生,則分數大小于![]() 分的概率為
分的概率為
![]() .
.
(![]() )由頻率分布直方圖可得文科四個班數學成績的平均分為
)由頻率分布直方圖可得文科四個班數學成績的平均分為
![]() ,
,
故平均成績為![]() 分.
分.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:
【題目】下列結論中正確的是__________.
①將一組數據中的每個數據都加上或減去同一個常數后,方差不變;
②在吸煙與患肺病這兩個分類變量的獨立性檢驗中,“有99%的把握認為吸煙與患肺病有關”的含義是“若某人吸煙,則他有99%的可能患肺病;”
③已知“![]() ”為真命題,則“
”為真命題,則“![]() ”、“
”、“![]() ”、“
”、“![]() ”中至少有一個真命題;
”中至少有一個真命題;
④以模型![]() 去擬合一組數據時,為了求出回歸方程,設
去擬合一組數據時,為了求出回歸方程,設![]() ,其變換后得到線性回歸方程
,其變換后得到線性回歸方程![]() 則
則![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 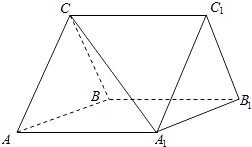
(1)證明AB⊥A1C;
(2)若平面ABC⊥平面AA1B1B,AB=CB,求直線A1C與平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4﹣5:不等式選講)
已知函數f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)當a=﹣2時,求不等式f(x)<g(x)的解集;
(2)設a>﹣1,且當 ![]() 時,f(x)≤g(x),求a的取值范圍.
時,f(x)≤g(x),求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中有四張卡片,分別寫有“瓷、都、文、明”四個字,有放回地從中任取一張卡片,將三次抽取后“瓷”“都”兩個字都取到記為事件![]() ,用隨機模擬的方法估計事件
,用隨機模擬的方法估計事件![]() 發生的概率.利用電腦隨機產生整數0,1,2,3四個隨機數,分別代表“瓷、都、文、明”這四個字,以每三個隨機數為一組,表示取卡片三次的結果,經隨機模擬產生了以下18組隨機數:
發生的概率.利用電腦隨機產生整數0,1,2,3四個隨機數,分別代表“瓷、都、文、明”這四個字,以每三個隨機數為一組,表示取卡片三次的結果,經隨機模擬產生了以下18組隨機數:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估計事件![]() 發生的概率為( )
發生的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求證:數列![]() 是等差數列,求數列
是等差數列,求數列![]() 的通項公式;
的通項公式;
(3)若![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,
, ![]() 都是從0,1,2,3,4五個數中任取的一個數,求上述函數有零點的概率;
都是從0,1,2,3,4五個數中任取的一個數,求上述函數有零點的概率;
(2)若![]() ,
, ![]() 都是從區間
都是從區間![]() 上任取的一個數,求
上任取的一個數,求![]() 成立的概率.
成立的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com