【題目】某市在爭創(chuàng)文明城市過程中，為調查市民對文明出行機動車禮讓行人的態(tài)度，選了某小區(qū)的100位居民調查結果統(tǒng)計如下：
支持 | 不支持 | 合計 | |
年齡不大于45歲 | 80 | ||
年齡大于45歲 | 10 | ||
合計 | 70 | 100 |
（1）根據(jù)已有數(shù)據(jù)，把表格數(shù)據(jù)填寫完整；
（2）能否在犯錯誤的概率不超過5%的前提下認為不同年齡段與是否支持文明出行機動車禮讓行人有關？
（3）已知在被調查的年齡小于25歲的支持者有5人，其中2人是教師，現(xiàn)從這5人中隨機抽取3人，求至多抽到1位教師的概率.
【答案】(1)見解析 (2) 能在犯錯誤的概率不超過5%的前提下認為不同年齡與是否支持文明出行有關(3) 
【解析】
（1）根據(jù)條件中所給的數(shù)據(jù)，列出列聯(lián)表，填上對應的數(shù)據(jù)即可；（2）假設沒有關系，根據(jù)列聯(lián)表把求得的數(shù)據(jù)代入觀測值的公式求出觀測值，把觀測值同臨界值進行比較得到結論；（3）列舉法確定基本事件即可求出概率.
解：（1）
支持 | 不支持 | 合計 | |
年齡不大于55歲 | 20 | 60 | 80 |
年齡大于55歲 | 10 | 10 | 20 |
合計 | 30 | 70 | 100 |
（2）
所以能在犯錯誤的概率不超過5%的前提下認為不同年齡與是否支持文明出行有關.
（3）記5人為a，b，c，d，e，a，b表示教師，從5人任意抽3人的所有等可能事件是：
abc，abd，abe，acd，ace，ade，bcd，bce，bde，cde共10個，其中“至多1位教
師”含有7個基本事件，所以所求概率
科目：高中數(shù)學 來源： 題型：
【題目】對于無窮數(shù)列
，
，若
－
…，則稱是的“收縮數(shù)列”.其中，
，
分別表示
中的最大數(shù)和最小數(shù).已知為無窮數(shù)列，其前
項和為
，數(shù)列是的“收縮數(shù)列”.
（1）若
，求的前項和；
（2）證明：的“收縮數(shù)列”仍是；
（3）若
，求所有滿足該條件的.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，正三角形ABE與菱形ABCD所在的平面互相垂直，
，
，M是AB的中點．
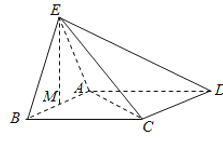
（1）求證:
;
（2）求二面角
的余弦值;
（3）在線段EC上是否存在點P，使得直線AP與平面ABE所成的角為
，若存在，求出
的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，直線l的參數(shù)方程為
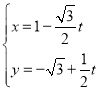（t為參數(shù)）.以坐標原點為極點，以x軸的正半軸為極軸，建立極坐標系.曲線C的極坐標方程為
.
（1）求直線l的普通方程及曲線C的直角坐標方程；
（2）設點
，直線l與曲線C相交于A，B兩點，求
的值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知四棱錐
中，底面
為菱形，且
，
，過側面
中線
的一個平面
與直線
垂直，并與此四棱錐的面相交，交線圍成一個平面圖形.
（1）畫出這個平面圖形，并證明
平面；
（2）若
，求平面與平面
所成的銳二面角的余弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為了更好地支持“中小型企業(yè)”的發(fā)展，某市決定對部分企業(yè)的稅收進行適當?shù)臏p免，某機構調查了當?shù)氐闹行⌒推髽I(yè)年收入情況，并根據(jù)所得數(shù)據(jù)畫出了樣本的頻率分布直方圖，下面三個結論：
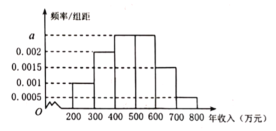
①樣本數(shù)據(jù)落在區(qū)間
的頻率為0.45；
②如果規(guī)定年收入在500萬元以內的企業(yè)才能享受減免稅政策，估計有55%的當?shù)刂行⌒推髽I(yè)能享受到減免稅政策；
③樣本的中位數(shù)為480萬元.
其中正確結論的個數(shù)為（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
， 
.
（1）當
時， 
在
上恒成立，求實數(shù)
的取值范圍；
（2）當
時，若函數(shù)
在
上恰有兩個不同的零點，求實數(shù)
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
