Question

【題目】甲、乙兩家商場對同一種商品開展促銷活動,對購買該商品的顧客兩家商場的獎勵方案如下:

甲商場:顧客轉動如圖所示的圓盤,當指針指向陰影部分(圖中兩個陰影部分均為扇形,且每個扇形的圓心角均為,邊界忽略不計)即為中獎.

乙商場:從裝有2個白球、2個藍球和2個紅球(這些球除顏色外完全相同)的盒子中一次性摸出2球,若摸到的是2個相同顏色的球,則為中獎.

試問:購買該商品的顧客在哪家商場中獎的可能性大?請說明理由.

Answer 1

【答案】答案見解析

【解析】試題分析：根據概率公式分別計算，由幾何概型概率公式求得P(A) . 由古典概型概率公式求得P(B)= 比較即可.

試題解析：設顧客去甲商場轉動圓盤,指針指向陰影部分為事件A,試驗的全部結果構成的區域為圓盤,面積為πr2(r為圓盤的半徑),陰影區域的面積為S=·π r2=π r2.由幾何概型概率公式,得P(A)= .

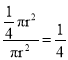設顧客去乙商場一次摸出兩個相同顏色的球為事件B,

記2個白球為白1,白2;2個紅球為紅1、紅2;2個藍球為藍1、藍2.

則從盒子中一次性摸出2球,一切可能的結果有:

(白1,白2),(白1,紅1)、(白1,紅2),(白1,藍1),(白1,藍2);

(白2,紅1),(白2,紅2),(白2,藍1),(白2,藍2);

(紅1,紅2),(紅1,藍1),(紅1,藍2);

(紅2,藍1),(紅2,藍2);

(藍1,藍2),共15種;

其中摸到的是2個相同顏色的球有(白1,白2),(紅1,紅2),(藍1,藍2),共3種;

由古典概型概率公式,得P(B)= .