Question

13．如圖所示給出的是計算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一個程序框圖，其中判斷框內應填入的條件是（　　）

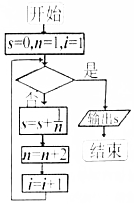
• A． i＞1010
• B． i＜1010
• C． i＞1009
• D． i＜1009

Answer 1

分析 由題意可知，首先是判斷框中的條件不滿足，所以框圖依次執行循環，框圖執行第一次循環后，S的值為1，執行第二次循環后，S的值為前2項的和，滿足S=1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$，框圖應執行1009次循環，此時i的值為1010，判斷框中的條件應該滿足，算法結束，由此得到判斷框中的條件．

解答 解：框圖首先給累加變量S賦值為0，n賦值1，給循環變量i賦值1．
判斷，判斷框中的條件不滿足，執行S=0+1，n=1+2=3，i=1+1=2；
判斷，判斷框中的條件不滿足，執行S=0+1+$\frac{1}{3}$，n=3+2=5，i=2+1=3；
判斷，判斷框中的條件不滿足，執行S=0+1+$\frac{1}{3}$+$\frac{1}{5}$，n=5+2=7，i=3+1=4；
…
判斷，判斷框中的條件不滿足，執行S=0+1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{19}$，n=19+2=21，i=10+1=11；
…，
判斷，判斷框中的條件不滿足，執行S=0+1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{19}$+…+$\frac{1}{2017}$，n=2017+2=2019，i=1009+1=1010；
判斷1010＞1009成立，跳出循環，輸出S的值為S=1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{19}$+…+$\frac{1}{2017}$，
故判斷框內應填入的一個條件為i＞1009，
故選：C．

點評 本題考查了循環結構，是直到型循環，區別當型和直到型的關鍵在于是滿足條件執行循環還是不滿足條件執行循環，滿足條件執行循環的是當型結構，不滿足條件執行循環的是直到型結構．