Question

設進入某商場的每一位顧客購買甲種商品的概率為0.5，購買乙種商品的概率為0.6， 且購買甲種商品與購買乙種商品相互獨立，各顧客之間購買商品也是相互獨立的.

（1）求進入商場的1位顧客至少購買甲、乙兩種商品中的一種的概率；

（2）記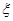表示進入商場的3位顧客中至少購買甲、乙兩種商品中的一種的人數，求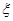的分布列及期望.

 

Answer 1

【答案】

(1)0.8;(2)2.4

【解析】

試題分析：(1)因為每一位顧客購買甲種商品的概率為0.5，購買乙種商品的概率為0.6，所以要求進入商場的1位顧客至少購買甲、乙兩種商品中的一種的概率可以利用對立事件來解決，即1減去甲、乙都沒購買的概率（1-0.5）（1-0.6），即可得所求的結論.

（2）由（1）可得每1位顧客至少購買甲、乙兩種商品中的一種的概率為0.8.所以對三位顧客中至少購買甲、乙兩種商品中的一種的人數的分為0,1,2,3四種情況.利用幾何概型可求得相應的概率，再利用數學期望的公式即可得結論.

試題解析：

（1）

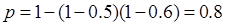
 （2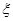）取值有0、1、2、3

 

 

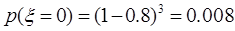
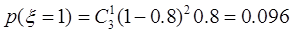
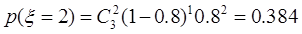
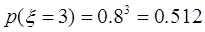
分布列為

	0	1	2	3
	0.008	0.096	0.384	0.512

 

 E(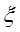)=3×0.8=2.4

考點：1.概率的概念.2.分布列的公式.3.事件的互斥或對立.