
【題目】已知曲線![]() ,直線
,直線![]() (其中
(其中![]() )與曲線
)與曲線![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
(Ⅰ)若![]() ,試判斷曲線
,試判斷曲線![]() 的形狀.
的形狀.
(Ⅱ)若![]() ,以線段
,以線段![]() 、
、![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,其中頂點
,其中頂點![]() 在曲線
在曲線![]() 上,
上, ![]() 為坐標原點,求
為坐標原點,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)答案見解析;(Ⅱ) ![]() .
.
【解析】試題分析:
(Ⅰ)結合所給的方程討論可得:
當![]() 時,曲線
時,曲線![]() 的形狀為直線
的形狀為直線![]() ,
,
當![]() 時,曲線表示以焦點在
時,曲線表示以焦點在![]() 軸上,以
軸上,以![]() 為實軸,以
為實軸,以![]() 為焦距的雙曲線,
為焦距的雙曲線,
當![]() 時,表示焦點在
時,表示焦點在![]() 軸上,以
軸上,以![]() 為長軸,以
為長軸,以![]() 為焦距的橢圓,
為焦距的橢圓,
當![]() 時,表示焦點在
時,表示焦點在![]() 軸上,以
軸上,以![]() 為長軸,以
為長軸,以![]() 為焦距的橢圓,
為焦距的橢圓,
當![]() 時,表示圓心在原點,以
時,表示圓心在原點,以![]() 為半徑的圓.
為半徑的圓.
(Ⅱ)當![]() 時,曲線方程為:
時,曲線方程為: ![]() ,分類討論:
,分類討論:
當![]() 時,
時, ![]() ,
,
當![]() 時,聯立直線與橢圓的方程,消去
時,聯立直線與橢圓的方程,消去![]() 整理變形,結合題意可得
整理變形,結合題意可得![]() ,結合
,結合![]() ,可得
,可得![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:
(Ⅰ)當![]() 時,
時, ![]() ,
, ![]() ,曲線
,曲線![]() 的形狀為直線
的形狀為直線![]() ,
,
當![]() 時,
時, ![]() ,表示以焦點在
,表示以焦點在![]() 軸上,以
軸上,以![]() 為實軸,
為實軸,
以![]() 為焦距的雙曲線,
為焦距的雙曲線,
當![]() 時,
時, ![]() ,
,
當![]() ,即
,即![]() 時,表示焦點在
時,表示焦點在![]() 軸上,以
軸上,以![]() 為長軸,以
為長軸,以![]() 為焦距的橢圓,
為焦距的橢圓,
當![]() ,即
,即![]() 時,表示焦點在
時,表示焦點在![]() 軸上,以
軸上,以![]() 為長軸,以
為長軸,以![]() 為焦距的橢圓,
為焦距的橢圓,
當![]() ,即
,即![]() 時,表示圓心在原點,以
時,表示圓心在原點,以![]() 為半徑的圓.
為半徑的圓.
(Ⅱ)當![]() 時,曲線方程為:
時,曲線方程為: ![]() ,
,
當![]() 時,
時, ![]() 在橢圓
在橢圓![]() 上,計算得出
上,計算得出![]() ,
,
∴![]() ,
,
當![]() 時,則
時,則 ,消去
,消去![]() 化簡整理得:
化簡整理得:
![]() ,
,
![]() ①,
①,
設![]() ,
, ![]() ,
, ![]() 的坐標分別為
的坐標分別為![]() ,
, ![]() ,
, ![]() ,
,
則![]() ,
, ![]() ,
,
因為點![]() 在橢圓
在橢圓![]() 上,所以
上,所以![]() ,
,
從而 ,化簡得:
,化簡得: ![]() ,
,
經檢驗滿足①式,
又![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
綜上, ![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為[40,50],[50,60],…,[80,90],[90,100] 
(1)求頻率分布圖中a的值;
(2)估計該企業的職工對該部門評分不低于80的概率;
(3)從評分在[40,60]的受訪職工中,隨機抽取2人,求此2人評分都在[40,50]的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() =(cosx,﹣
=(cosx,﹣ ![]() ),
), ![]() =(sinx+cosx,1),f(x)=
=(sinx+cosx,1),f(x)= ![]()
![]() ,
,
(1)若0<α< ![]() ,sinα=
,sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函數f(x)的最小正周期及單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),在同一周期內,當x= ![]() 時,f(x)取得最大值3;當x=
時,f(x)取得最大值3;當x= ![]() 時,f(x)取得最小值﹣3.
時,f(x)取得最小值﹣3.
(1)求函數f(x)的解析式;
(2)求函數f(x)的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是等差數列,{bn}是各項都為正數的等比數列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通項公式;
(2)求數列 ![]() 的前n項和Sn .
的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中, ![]() ,
, ![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉成
翻轉成![]() .若
.若![]() 為線段
為線段![]() 的中點,則在
的中點,則在![]() 翻折過程中:
翻折過程中:
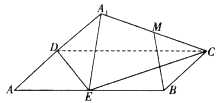
①![]() 是定值;②點
是定值;②點![]() 在某個球面上運動;
在某個球面上運動;
③存在某個位置,使![]() ;④存在某個位置,使
;④存在某個位置,使![]() 平面
平面![]() .
.
其中正確的命題是_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com