
【題目】求定積分![]() 的值.
的值.
【答案】【解答】![]() 表示圓(x-1)2+y2=1(y≥0)的一部分與直線y=x所圍成的圖形的面積,故原式=
表示圓(x-1)2+y2=1(y≥0)的一部分與直線y=x所圍成的圖形的面積,故原式=![]() ×π×12-
×π×12- ![]() ×1×1=
×1×1=![]()
【解析】利用定積分的幾何意義求定積分的方法步驟:(1)確定被積函數(shù)和積分區(qū)間.(2)準(zhǔn)確畫出圖形.(3)求出各部分的面積.(4)寫出定積分,注意當(dāng)f(x)≥0時,S= ![]() f(x)dx , 而當(dāng)f(x)≤0時,S=-
f(x)dx , 而當(dāng)f(x)≤0時,S=- ![]() f(x)dx . ;利用定積分的幾何意義求定積分的注意點:準(zhǔn)確理解其幾何意義,同時要合理利用函數(shù)的奇偶性.對稱性來解決問題.另外,要注意結(jié)合圖形的直觀輔助作用.
f(x)dx . ;利用定積分的幾何意義求定積分的注意點:準(zhǔn)確理解其幾何意義,同時要合理利用函數(shù)的奇偶性.對稱性來解決問題.另外,要注意結(jié)合圖形的直觀輔助作用.
【考點精析】認(rèn)真審題,首先需要了解定積分的概念(定積分的值是一個常數(shù),可正、可負(fù)、可為零;用定義求定積分的四個基本步驟:①分割;②近似代替;③求和;④取極限).


科目:高中數(shù)學(xué) 來源: 題型:
【題目】假設(shè)要抽查某企業(yè)生產(chǎn)的某種品牌的袋裝牛奶的質(zhì)量是否達(dá)標(biāo),現(xiàn)從700袋牛奶中抽取50袋進(jìn)行檢驗.利用隨機數(shù)表抽取樣本時,先將700袋牛奶按001,002,…,700進(jìn)行編號,如果從隨機數(shù)表第3行第1組數(shù)開始向右讀,最先讀到的5袋牛奶的編號是614,593,379,242,203,請你以此方式繼續(xù)向右讀數(shù),隨后讀出的3袋牛奶的編號是 . (下列摘取了隨機數(shù)表第1行至第5行) 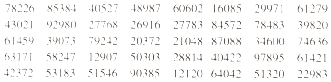
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 在其定義域內(nèi)為增函數(shù),求
在其定義域內(nèi)為增函數(shù),求![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,設(shè)函數(shù)![]() ,若在
,若在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】用數(shù)學(xué)歸納法證明命題“當(dāng)n是正奇數(shù)時,xn+yn能被x+y整除”,在第二步的證明時,正確的證法是( )
A.假設(shè)n=k(k∈N*)時命題成立,證明n=k+1時命題也成立
B.假設(shè)n=k(k是正奇數(shù))時命題成立,證明n=k+1時命題也成立
C.假設(shè)n=k(k是正奇數(shù))時命題成立,證明n=k+2時命題也成立
D.假設(shè)n=2k+1(k∈N)時命題成立,證明n=k+1時命題也成立
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知正四棱柱![]() 中,底面邊長
中,底面邊長![]() ,側(cè)棱
,側(cè)棱![]() 的長為4,過點
的長為4,過點![]() 作
作![]() 的垂線交側(cè)棱
的垂線交側(cè)棱![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
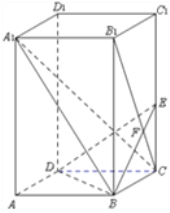
(1)求證: ![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè) ![]() 個正數(shù)
個正數(shù) ![]() 滿足
滿足 ![]() (
( ![]() 且
且 ![]() ).
).
(1)當(dāng) ![]() 時,證明:
時,證明: ![]() ;
;
(2)當(dāng) ![]() 時,不等式
時,不等式 ![]() 也成立,請你將其推廣到
也成立,請你將其推廣到 ![]() (
( ![]() 且
且 ![]() )個正數(shù)
)個正數(shù) ![]() 的情形,歸納出一般性的結(jié)論并用數(shù)學(xué)歸納法證明.
的情形,歸納出一般性的結(jié)論并用數(shù)學(xué)歸納法證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標(biāo)系,曲線
軸正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知點![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于不同的兩點
相交于不同的兩點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)是定義在R上的奇函數(shù),且當(dāng)x>0時,f(x)=x2+2x.
(Ⅰ)求f(0)的值;
(Ⅱ)求此函數(shù)在R上的解析式;
(Ⅲ)若對任意的t∈R,不等式f(t+1)+f(m﹣2t2)<0恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com