
【題目】某商場銷售某種品牌的空調器,每周周初購進一定數量的空調器,商場沒銷售一臺空調器可獲利500元,若供大于求,則每臺多余的空調器需交保管費100元;若供不應求,則可從其他商店調劑供應,此時每臺空調器僅獲利潤200元.
(Ⅰ)若該商場周初購進20臺空調器,求當周的利潤(單位:元)關于當周需求量![]() (單位:臺,
(單位:臺,![]() )的函數解析式
)的函數解析式![]() ;
;
(Ⅱ)該商場記錄了去年夏天(共10周)空調器需求量(單位:臺),整理得下表:

以10周記錄的各需求量的頻率作為各需求量發生的概率,若商場周初購進20臺空調器,![]() 表示當周的利潤(單位:元),求
表示當周的利潤(單位:元),求![]() 的分布及數學期望.
的分布及數學期望.
科目:高中數學 來源: 題型:
【題目】如圖1,在高為2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,過
,過![]() 、
、![]() 分別作
分別作![]() ,
, ![]() ,垂足分別為
,垂足分別為![]() 、
、![]() 。已知
。已知![]() ,將梯形
,將梯形![]() 沿
沿![]() 、
、![]() 同側折起,得空間幾何體
同側折起,得空間幾何體![]() ,如圖2。
,如圖2。

(1)若![]() ,證明:
,證明: ![]() ;
;
(2)若![]() ,證明:
,證明: ![]() ;
;
(3)在(1),(2)的條件下,求三棱錐![]() 的體積。
的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三共有2000名學生參加廣安市聯考,現隨機抽取100名學生的成績(單位:分),并列成如下表所示的頻數分布表:
組別 |
|
|
|
|
|
|
頻數 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)試估計該年級成績![]() 分的學生人數;
分的學生人數;
(2)已知樣本中成績在![]() 中的6名學生中,有4名男生,2名女生,現從中選2人進行調研,求恰好選中一名男生一名女生的概率.
中的6名學生中,有4名男生,2名女生,現從中選2人進行調研,求恰好選中一名男生一名女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年天貓五一活動結束后,某地區研究人員為了研究該地區在五一活動中消費超過3000元的人群的年齡狀況,隨機在當地消費超過3000元的群眾中抽取了500人作調查,所得概率分布直方圖如圖所示:記年齡在![]() ,
, ![]() ,
, ![]() 對應的小矩形的面積分別是
對應的小矩形的面積分別是![]() ,且
,且![]() .
.
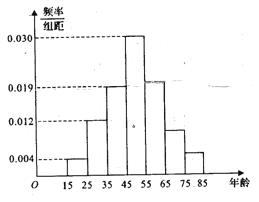
(1)以頻率作為概率,若該地區五一消費超過3000元的有30000人,試估計該地區在五一活動中消費超過3000元且年齡在![]() 的人數;
的人數;
(2)計算在五一活動中消費超過3000元的消費者的平均年齡;
(3)若按照分層抽樣,從年齡在![]() ,
, ![]() 的人群中共抽取7人,再從這7人中隨機抽取2人作深入調查,求至少有1人的年齡在
的人群中共抽取7人,再從這7人中隨機抽取2人作深入調查,求至少有1人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前n項和為Sn,點
的前n項和為Sn,點![]() 在直線
在直線![]() 上,數列
上,數列![]() 為等差數列,且
為等差數列,且![]() ,前9項和為153.
,前9項和為153.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)設![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,求使不等式
,求使不等式![]() 對一切的
對一切的![]() 都成立的最大整數k.
都成立的最大整數k.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P(2,0),且圓C:x2+y2﹣6x+4y+4=0.
(Ⅰ)當直線![]() 過點P且與圓心C的距離為1時,求直線
過點P且與圓心C的距離為1時,求直線![]() 的方程;
的方程;
(Ⅱ)設過點P的直線與圓C交于A、B兩點,若|AB|=4,求以線段AB為直徑的圓的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com