
設(shè)項數(shù)均為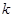 (
(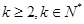 )的數(shù)列
)的數(shù)列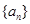 、
、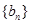 、
、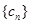 前
前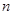 項的和分別為
項的和分別為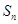 、
、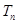 、
、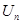 .已知集合
.已知集合 =
=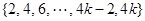 .
.
(1)已知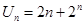 ,求數(shù)列
,求數(shù)列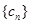 的通項公式;
的通項公式;
(2)若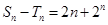
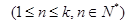 ,試研究
,試研究 和
和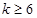 時是否存在符合條件的數(shù)列對(
時是否存在符合條件的數(shù)列對(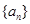 ,
,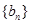 ),并說明理由;
),并說明理由;
(3)若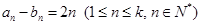 ,對于固定的
,對于固定的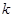 ,求證:符合條件的數(shù)列對(
,求證:符合條件的數(shù)列對(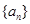 ,
,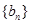 )有偶數(shù)對.
)有偶數(shù)對.
(1)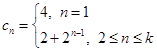 ;(2)
;(2) 時,數(shù)列
時,數(shù)列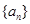 、
、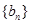 可以為(不唯一)6,12,16,14;2,8,10,4,
可以為(不唯一)6,12,16,14;2,8,10,4,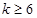 時,數(shù)列對(
時,數(shù)列對(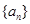 ,
,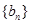 )不存在.(3)證明見解析.
)不存在.(3)證明見解析.
解析試題分析:(1)這實質(zhì)是已知數(shù)列的前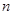 項和
項和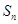 ,要求通項公式
,要求通項公式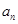 的問題,利用關(guān)系
的問題,利用關(guān)系 來解決;(2)
來解決;(2) 時,可求出
時,可求出 ,再利用
,再利用
=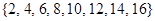 ,可找到數(shù)列對(
,可找到數(shù)列對(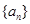 ,
,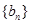 )(注意結(jié)果不唯一),當(dāng)
)(注意結(jié)果不唯一),當(dāng)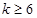 時,由于
時,由于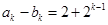 ,即
,即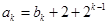 ,可以想象,若存在,則
,可以想象,若存在,則 應(yīng)該很大(體現(xiàn)在
應(yīng)該很大(體現(xiàn)在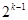 ),研究發(fā)現(xiàn)
),研究發(fā)現(xiàn)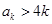 (具體證明可利用二項展開式,
(具體證明可利用二項展開式,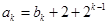
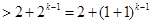



 ,注意到
,注意到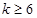 ,展開式中至少有7項,故
,展開式中至少有7項,故 ,下面證明這個式子大于
,下面證明這個式子大于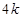 ,應(yīng)該很好證明了),這不符合題意,故不存在;(3)可通過構(gòu)造法說明滿足題意和數(shù)列對是成對出現(xiàn)的,即對于數(shù)列對(
,應(yīng)該很好證明了),這不符合題意,故不存在;(3)可通過構(gòu)造法說明滿足題意和數(shù)列對是成對出現(xiàn)的,即對于數(shù)列對(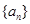 ,
,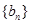 ),構(gòu)造新數(shù)列對
),構(gòu)造新數(shù)列對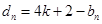 ,
, (
(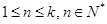 ),則數(shù)列對(
),則數(shù)列對(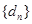 ,
,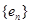 )也滿足題意,(要說明的是
)也滿足題意,(要說明的是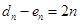 及
及 =
=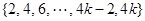 且數(shù)列
且數(shù)列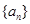 與
與 ,
,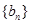 與
與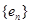 不相同(用反證法,若相同,則
不相同(用反證法,若相同,則 ,又
,又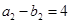 ,則有
,則有 均為奇數(shù),矛盾).
均為奇數(shù),矛盾).
試題解析:(1)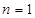 時,
時,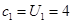
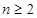 時,
時, ,
,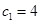 不適合該式
不適合該式
故,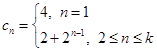 4分
4分
(2) ,
,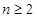 時,
時,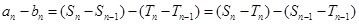
 6分
6分
當(dāng) 時,
時, ,
,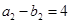 ,
, ,
,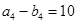
 =
=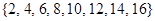
數(shù)列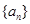 、
、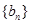 可以為(不唯一):
可以為(不唯一):
6,12,16,14;2,8,10,4 ② 16,10,8,14;12,6,2,4 8分
當(dāng)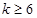 時,
時,

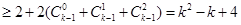
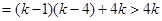
此時 不存在.故數(shù)列對(
不存在.故數(shù)列對(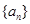 ,
,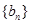 )不存在. &
)不存在. &


 學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案
學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案 Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示的兩個同心圓盤均被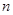 等分(
等分(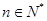 且
且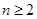 ),在相重疊的扇形格中依次同時填上
),在相重疊的扇形格中依次同時填上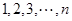 ,內(nèi)圓盤可繞圓心旋轉(zhuǎn),每次可旋轉(zhuǎn)一個扇形格,當(dāng)內(nèi)圓盤旋轉(zhuǎn)到某一位置時,定義所有重疊扇形格中兩數(shù)之積的和為此位置的“旋轉(zhuǎn)和”.
,內(nèi)圓盤可繞圓心旋轉(zhuǎn),每次可旋轉(zhuǎn)一個扇形格,當(dāng)內(nèi)圓盤旋轉(zhuǎn)到某一位置時,定義所有重疊扇形格中兩數(shù)之積的和為此位置的“旋轉(zhuǎn)和”.
(1)求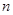 個不同位置的“旋轉(zhuǎn)和”的和;
個不同位置的“旋轉(zhuǎn)和”的和;
(2)當(dāng)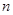 為偶數(shù)時,求
為偶數(shù)時,求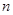 個不同位置的“旋轉(zhuǎn)和”的最小值;
個不同位置的“旋轉(zhuǎn)和”的最小值;
(3)設(shè)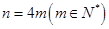 ,在如圖所示的初始位置將任意
,在如圖所示的初始位置將任意 對重疊的扇形格中的兩數(shù)均改寫為0,證明:當(dāng)
對重疊的扇形格中的兩數(shù)均改寫為0,證明:當(dāng)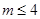 時,通過旋轉(zhuǎn),總存在一個位置,任意重疊的扇形格中兩數(shù)不同時為0.
時,通過旋轉(zhuǎn),總存在一個位置,任意重疊的扇形格中兩數(shù)不同時為0.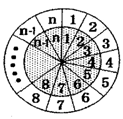
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列 的各項都是正數(shù),且對任意
的各項都是正數(shù),且對任意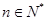 都有
都有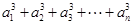
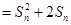 ,其中
,其中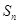 為數(shù)列
為數(shù)列 的前
的前 項和.
項和.
(1)求 、
、 ;
;
(2)求數(shù)列 的通項公式;
的通項公式;
(3)設(shè)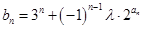 ,對任意的
,對任意的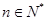 ,都有
,都有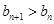 恒成立,求實數(shù)
恒成立,求實數(shù)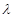 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
在等差數(shù)列{an}中,若a3+a4+a5+a6+a7=450,則a1+a9的值等于( )
| A.45 | B.75 | C.180 | D.300 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com