【題目】電子計算機誕生于20世紀中葉，是人類最偉大的技術發明之一．計算機利用二進制存儲信息，其中最基本單位是“位(bit)”，1位只能存放2種不同的信息：0或l，分別通過電路的斷或通實現．“字節(Byte)”是更大的存儲單位，1Byte=8bit，因此1字節可存放從00000000(2)至11111111(2)共256種不同的信息．將這256個二進制數中，所有恰有相鄰兩位數是1其余各位數均是0的所有數相加，則計算結果用十進制表示為
A. 254B. 381C. 510D. 765
尖子生新課堂課時作業系列答案科目：高中數學 來源： 題型：
【題目】已知點Q是圓
上的動點，點
，若線段QN的垂直平分線MQ于點P.
(I)求動點P的軌跡E的方程
(II)若A是軌跡E的左頂點，過點D（-3，8）的直線l與軌跡E交于B，C兩點，求證：直線AB、AC的斜率之和為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種大型醫療檢查機器生產商，對一次性購買2臺機器的客戶，推出兩種超過質保期后兩年內的延保維修優惠方案：方案一：交納延保金7000元，在延保的兩年內可免費維修2次，超過2次每次收取維修費2000元；方案二：交納延保金10000元，在延保的兩年內可免費維修4次，超過4次每次收取維修費1000元.某醫院準備一次性購買2臺這種機器。現需決策在購買機器時應購買哪種延保方案，為此搜集并整理了50臺這種機器超過質保期后延保兩年內維修的次數，得下表：
維修次數 | 0 | 1 | 2 | 3 |
臺數 | 5 | 10 | 20 | 15 |
以這50臺機器維修次數的頻率代替1臺機器維修次數發生的概率，記X表示這2臺機器超過質保期后延保的兩年內共需維修的次數。
（1）求X的分布列；
（2）以所需延保金及維修費用的期望值為決策依據，醫院選擇哪種延保方案更合算？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某公司生產線生產的某種產品中抽取
件，測量這些產品的一項質量指標，由檢測結果得如圖所示的頻率分布直方圖：
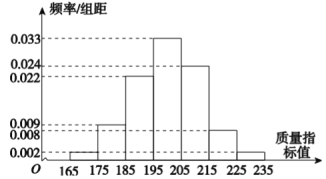
（Ⅰ）求這件產品質量指標的樣本平均數
和樣本方差
（同一組中的數據用該組區間的中點值作代表）；
（Ⅱ）由直方圖可以認為，這種產品的質量指標值
服從正態分布
，其中
近似為樣本平均數
近似為樣本方差.
（i）利用該正態分布，求
；
（ii）已知每件該產品的生產成本為
元，每件合格品（質量指標值
）的定價為
元；若為次品（質量指標值
），除了全額退款外且每件次品還須賠付客戶
元。若該公司賣出
件這種產品，記
表示這件產品的利潤，求
.
附：
.若
，則
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，AE⊥平面ABCD，CF∥AE，AD∥BC，AD⊥AB，AB=AD=1，AE=BC=2.
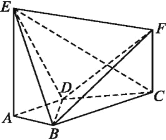
（1）求證：BF∥平面ADE；
（2）若二面角E-BD-F的余弦值為
，求線段CF的長.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設等差數列
的公差
,前
項和為
,且滿足
,
（1）試尋找一個等差數列
和一個非負常數
,使得等式
對于任意的正整數恒成立,并說明你的理由；
（2）對于（1）中的等差數列和非負常數,試求
（
）的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
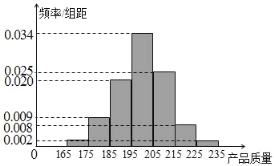
【題目】某企業為了檢查甲、乙兩條自動包裝流水線的生產情況，隨機在這兩條流水線上各抽取100件產品作為樣本稱出它們的質量（單位：毫克），質量值落在
的產品為合格品，否則為不合格品．如表是甲流水線樣本頻數分布表，如圖是乙流水線樣本的頻率分布直方圖．
產品質量/毫克 | 頻數 |
（165，175] | 3 |
（175，185] | 2 |
（185，195] | 21 |
（195，205] | 36 |
（205，215] | 24 |
（215，225] | 9 |
（225，235] | 5 |
（Ⅰ）根據乙流水線樣本的頻率分布直方圖，求乙流水線樣本質量的中位數（結果保留整數）；
（Ⅱ）從甲流水線樣本中質量在
的產品中任取2件產品，求兩件產品中恰有一件合格品的概率；
甲流水線 | 乙流水線 | 總計 | |
合格品 | |||
不合格品 | |||
總計 |
（Ⅲ）由以上統計數據完成下面2×2列聯表，能否在犯錯誤的概率不超過0.15的前提下認為產品的包裝合格與兩條自動包裝流水線的選擇有關？
下面臨界值表僅供參考：
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式：
，其中n＝a+b+c+d．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐PABC中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M為線段AD上一點，AM=2MD，N為PC的中點.
（Ⅰ）證明MN∥平面PAB;
（Ⅱ）求直線AN與平面PMN所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知過定點
的動圓是
與圓
相內切.
（1）求動圓圓心的軌跡方程；
（2）設動圓圓心的軌跡為曲線
，
是曲線上的兩點，線段
的垂直平分線過點
，求
面積的最大值（
是坐標原點）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
