
【題目】已知函數![]() .
.
(1)若函數![]() 存在不小于
存在不小于![]() 的極小值,求實數
的極小值,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,若對
時,若對![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用導數分析函數![]() 的單調性,求出函數
的單調性,求出函數![]() 的極值,然后令極值大于等于
的極值,然后令極值大于等于![]() ,解出不等式可得出實數
,解出不等式可得出實數![]() 的取值范圍;
的取值范圍;
(2)構造函數![]() ,問題等價于
,問題等價于![]() ,對實數
,對實數![]() 進行分類討論,分析函數
進行分類討論,分析函數![]() 在區間
在區間![]() 上的單調性,結合條件
上的單調性,結合條件![]() 可得出實數
可得出實數![]() 的取值范圍.
的取值范圍.
(1)函數![]() 的定義域為
的定義域為![]() ,
,![]() .
.
當![]() 時,
時,![]() ,函數
,函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
此時,函數![]() 無極值;
無極值;
當![]() 時,令
時,令![]() ,得
,得![]() ,
,
又當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以,函數![]() 在
在![]() 時取得極小值,且極小值為
時取得極小值,且極小值為![]() .
.
令![]() ,即
,即![]() ,得
,得![]() .
.
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]() ;
;
(2)當![]() 時,問題等價于
時,問題等價于![]() ,
,
記![]() ,
,
由(1)知,![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
所以![]() 在區間
在區間![]() 上單調遞增,所以
上單調遞增,所以![]() ,
,
①當![]() 時,由
時,由![]() 可知,所以
可知,所以![]() 成立;
成立;
②當![]() 時,
時,![]() 的導函數為
的導函數為![]() 恒成立,所以
恒成立,所以![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
所以![]() .
.
所以,函數![]() 在區間
在區間![]() 上單調遞增,從而
上單調遞增,從而![]() ,命題成立.
,命題成立.
③當![]() 時,顯然
時,顯然![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
記![]() ,則
,則![]() ,當
,當![]() 時,
時,![]() ,
,
所以,函數![]() 在區間
在區間![]() 上為增函數,即當
上為增函數,即當![]() 時,
時,![]() .
.
![]() ,
,![]() ,
,
所以在區間![]() 內,存在唯一的
內,存在唯一的![]() ,使得
,使得![]() ,
,
且當![]() 時,
時,![]() ,即當
,即當![]() 時,
時,![]() ,不符合題意,舍去.
,不符合題意,舍去.
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】某研究機構為了了解各年齡層對高考改革方案的關注程度,隨機選取了200名年齡在![]() 內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分第一~五組區間分別為
內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分第一~五組區間分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
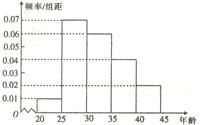
(1)求選取的市民年齡在![]() 內的人數;
內的人數;
(2)若從第3,4組用分層抽樣的方法選取5名市民進行座談,再從中選取2人在座談會中作重點發言,求作重點發言的市民中至少有一人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天氣預報說,在今后的三天中,每天下雨的概率都為![]() .現采用隨機模擬試驗的方法估計這三天中恰有兩天下雨的概率:用
.現采用隨機模擬試驗的方法估計這三天中恰有兩天下雨的概率:用![]() 表示下雨,從下列隨機數表的第
表示下雨,從下列隨機數表的第![]() 行第
行第![]() 列的
列的![]() 開始讀取,直到讀取了
開始讀取,直到讀取了![]() 組數據,
組數據,
18 18 07 92 45 44 17 16 58 09 79 83 86 19 62 06 76 50 03 10
55 23 64 05 05 26 62 38 97 75 34 16 07 44 99 83 11 46 32 24
據此估計,這三天中恰有兩天下雨的概率近似為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在統計學中,偏差是指個別測定值與測定的平均值之差,在成績統計中,我們把某個同學的某刻考試成績與該科班平均分的差叫某科偏差,班主任為了了解個別學生的偏科情況,對學生數學偏差![]() (單位:分)與物理偏差
(單位:分)與物理偏差![]() (單位:分)之間的關系進行偏差分析,決定從全班40位同學中隨機抽取一個容量為8的樣本進行分析,得到他們的兩科成績偏差數據如表:
(單位:分)之間的關系進行偏差分析,決定從全班40位同學中隨機抽取一個容量為8的樣本進行分析,得到他們的兩科成績偏差數據如表:

(1)已知![]() 與
與![]() 之間具有線性相關關系,求
之間具有線性相關關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若這次考試該班數學平均分為120分,物理平均分為92,試預測數學成績126分的同學的物理成績.
參考公式:  ,
, ![]()
參考數據: ![]() ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,C、D是以AB為直徑的圓上兩點,AB=2AD=2![]() ,AC=BC,F 是AB上一點,且AF=
,AC=BC,F 是AB上一點,且AF=![]() AB,將圓沿直徑AB折起,使點C在平面ABD的射影E在BD上,已知CE=
AB,將圓沿直徑AB折起,使點C在平面ABD的射影E在BD上,已知CE=![]() .
.

(1)求證:AD⊥平面BCE;
(2)求證:AD∥平面CEF;
(3)求三棱錐A﹣CFD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】寫出下列命題的否定,并判斷所得命題的真假:
(1)二次函數![]() 的圖像的頂點坐標是
的圖像的頂點坐標是![]() ;
;
(2)正數的立方根都是正數;
(3)存在一個最大的內角小于60°的三角形;
(4)對任意實數t,點![]() 都在一次函數
都在一次函數![]() 的圖像上.
的圖像上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com