
【題目】對于兩條平行直線![]() 、
、![]() (
(![]() 在
在![]() 下方)和圖象
下方)和圖象![]() 有如下操作:將圖象
有如下操作:將圖象![]() 在直線
在直線![]() 下方的部分沿直線
下方的部分沿直線![]() 翻折,其余部分保持不變,得到圖象
翻折,其余部分保持不變,得到圖象![]() ;將圖象
;將圖象![]() 在直線
在直線![]() 上方的部分沿直線
上方的部分沿直線![]() 翻折,其余部分保持不變,得到圖象
翻折,其余部分保持不變,得到圖象![]() :再將圖
:再將圖![]() 在直線下方的部分沿直線
在直線下方的部分沿直線![]() 翻折,其余部分保持不變,得到圖象
翻折,其余部分保持不變,得到圖象![]() ;再將圖象
;再將圖象![]() 在直線
在直線![]() 上方的部分沿直線
上方的部分沿直線![]() 翻折,其余部分保持不變,得到圖象
翻折,其余部分保持不變,得到圖象![]() ;以此類推…;直到圖象
;以此類推…;直到圖象![]() 上所有點均在
上所有點均在![]() 、
、![]() 之間(含
之間(含![]() 、
、![]() 上)操作停止,此時稱圖象
上)操作停止,此時稱圖象![]() 為圖象
為圖象![]() 關于直線
關于直線![]() 、
、![]() 的“衍生圖形”,線段
的“衍生圖形”,線段![]() 關于直線
關于直線![]() 、
、![]() 的“衍生圖形”為折線段
的“衍生圖形”為折線段![]() .
.
(1)直線型
平面直角坐標系中,設直線![]() ,直線
,直線![]()
①令圖象![]() 為
為![]() 的函數圖象,則圖象
的函數圖象,則圖象![]() 的解析式為
的解析式為
②令圖像![]() 為
為![]() 的函數圖象,請你畫出
的函數圖象,請你畫出![]() 和
和![]() 的圖象
的圖象

③若函數![]() 的圖象與圖象
的圖象與圖象![]() 有且僅有一個交點,且交點在
有且僅有一個交點,且交點在![]() 軸的左側,那么
軸的左側,那么![]() 的取值范圍是_______.
的取值范圍是_______.
④請你觀察圖象![]() 并描述其單調性,直接寫出結果_______.
并描述其單調性,直接寫出結果_______.
⑤請你觀察圖象![]() 并判斷其奇偶性,直接寫出結果_______.
并判斷其奇偶性,直接寫出結果_______.
⑥圖象![]() 所對應函數的零點為_______.
所對應函數的零點為_______.
⑦任取圖象![]() 中橫坐標
中橫坐標![]() 的點,那么在這個變化范圍中所能取到的最高點的坐標為(_______,_______),最低點坐標為(_______,_______).
的點,那么在這個變化范圍中所能取到的最高點的坐標為(_______,_______),最低點坐標為(_______,_______).
⑧若直線![]() 與圖象
與圖象![]() 有2個不同的交點,則
有2個不同的交點,則![]() 的取值范圍是_______.
的取值范圍是_______.
⑨根據函數圖象,請你寫出圖象![]() 的解析式_______.
的解析式_______.
(2)曲線型
若圖象![]() 為函數
為函數![]() 的圖象,
的圖象,
平面直角坐標系中,設直線![]() ,直線
,直線![]() ,
,
則我們可以很容易得到![]() 所對應的解析式為
所對應的解析式為![]() .
.

①請畫出![]() 的圖象,記
的圖象,記![]() 所對應的函數解析式為
所對應的函數解析式為![]() .
.
②函數![]() 的單調增區間為_______,單調減區間為_______.
的單調增區間為_______,單調減區間為_______.
③當![]() 時候,函數
時候,函數![]() 的最大值為_______,最小值為_______.
的最大值為_______,最小值為_______.
④若方程![]() 有四個不同的實數根,則
有四個不同的實數根,則![]() 的取值范圍為_______.
的取值范圍為_______.
(3)封閉圖形型
平面直角坐標系中,設直線![]() ,直線
,直線![]()
設圖象![]() 為四邊形
為四邊形![]() ,其頂點坐標分別為
,其頂點坐標分別為![]() ,
,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 關于直線
關于直線![]() 、
、![]() 的“衍生圖形”為
的“衍生圖形”為![]() .
.
①![]() 的周長為_______.
的周長為_______.
②若直線![]() 平分
平分![]() 的周長,則
的周長,則![]() _______.
_______.
③將![]() 沿右上方
沿右上方![]() 方向平移
方向平移![]() 個單位,則平移過程中
個單位,則平移過程中![]() 所掃過的面積為_______.
所掃過的面積為_______.
【答案】(1)①![]() ;②函數圖像見解析;③
;②函數圖像見解析;③![]() ;④
;④![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,
,![]() 的單調遞減區間為
的單調遞減區間為![]() ,
,![]() ;⑤偶函數;
;⑤偶函數;
⑥![]() ;⑦
;⑦![]() ,
,![]() ;⑧
;⑧![]()
⑨
(2)①詳圖見解析;②增區間![]() 和
和![]() ,減區間
,減區間![]() 和
和![]()
③最大值為12,最小值為0;④![]()
(3)①![]() ;②
;②![]() ;③
;③![]()
【解析】
通過對“衍生圖形”概念的理解,需要先定位兩條平行直線![]() 、
、![]() ,隨著平行直線的變化,“衍生圖形”最終也會發生相應的變化。
,隨著平行直線的變化,“衍生圖形”最終也會發生相應的變化。
解題過程中抓住兩個核心:只要是第奇數次翻折,那么圖像就要把位于![]() 下面的沿著
下面的沿著![]() 向上翻折;只要是第偶數次翻折,圖像就把位于
向上翻折;只要是第偶數次翻折,圖像就把位于![]() 上面的向下翻折,解題過程只要依據翻折的基本原理,結合函數的基本性質,逐步求解即可
上面的向下翻折,解題過程只要依據翻折的基本原理,結合函數的基本性質,逐步求解即可
首先對于(1)直線型
兩平行直線為直線![]() ,直線
,直線![]()
對①,當發生第一次翻折,![]() 的圖像相當于把
的圖像相當于把![]() 軸下方圖像沿著
軸下方圖像沿著![]() 軸向上翻折,此時應滿足
軸向上翻折,此時應滿足![]()
對②,圖像如圖所示
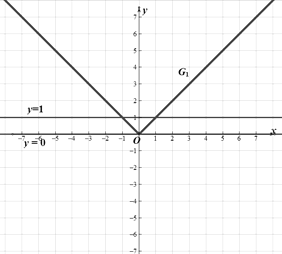
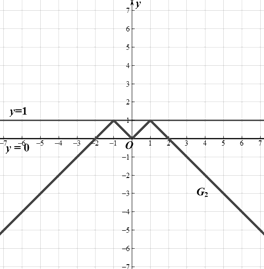
對③,![]() ,圖像恒過
,圖像恒過![]() ,又因
,又因![]() 與圖像
與圖像![]() 有且僅有一個交點,且交點在
有且僅有一個交點,且交點在![]() 軸的左側,如圖所示
軸的左側,如圖所示

若只有一個交點,應滿足![]()
對④,根據![]() 圖像,
圖像,![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]()
![]() 的單調遞減區間為
的單調遞減區間為![]() ,
,![]()
對⑤,![]() 圖像關于
圖像關于![]() 軸對稱,為偶函數
軸對稱,為偶函數
對⑥,![]() 圖像對應的零點為:
圖像對應的零點為:![]()
對⑦,![]() 圖像在
圖像在![]() 上的最高點的坐標為
上的最高點的坐標為![]() ,最低點的坐標為
,最低點的坐標為![]()
對⑧,若直線![]() 與圖象
與圖象![]() 有2個不同的交點,由圖像可知
有2個不同的交點,由圖像可知
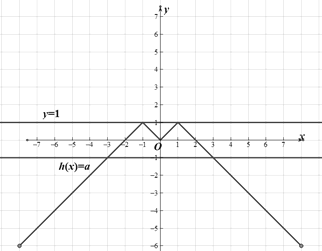
則![]()
對⑨,觀察圖像特點![]() 為偶函數,當
為偶函數,當![]() ,
,![]() ,當
,當![]() 和
和![]() 時,
時,![]() ,則
,則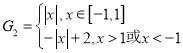
對于(2)曲線型
![]() ,
,![]() 所對應的解析式為
所對應的解析式為![]()
對①,圖像如圖所示
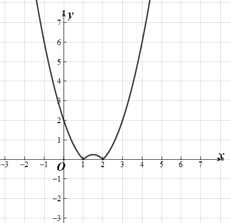
對②,函數的單調增區間為![]() 和
和![]() ,單調減區間為
,單調減區間為![]() 和
和![]()
對③,當![]() 時候,函數
時候,函數![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]()
對④,④若方程![]() 有四個不同的實數根,即等價于
有四個不同的實數根,即等價于![]() 與
與![]() 圖像有四個交點
圖像有四個交點
如圖所示:
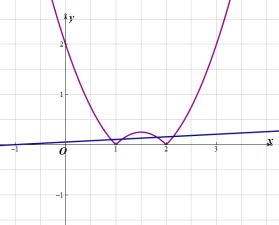
要使兩函數圖像有四個交點,應滿足 ,解得
,解得![]()
(3)封閉型曲線,根據題意先畫出四邊形的“衍生圖形”,
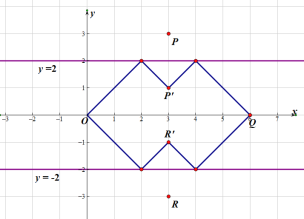
對①,![]() 的周長為
的周長為![]()
對②,
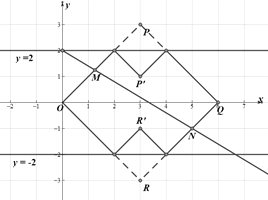
要使![]() 被直線
被直線![]() 平分周長,則假設直線與
平分周長,則假設直線與![]() 交點為
交點為![]() ,與直線
,與直線![]() 交點為
交點為![]() ,則應滿足
,則應滿足![]()
直線![]() 方程為:
方程為: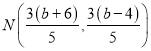 ,直線
,直線![]() 方程為:
方程為:![]()
聯立直線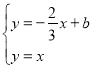 得
得![]() ,
,![]()
聯立直線 得
得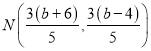 ,
,![]()
由![]() 得
得![]() ,解得
,解得![]()
對③,如圖所示
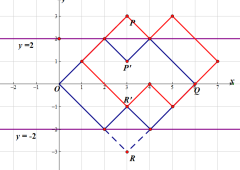
平移之后![]() 掃過的面積應為
掃過的面積應為![]()


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
【題目】某企業為打入國際市場,決定從![]() 、
、![]() 兩種產品中只選擇一種進行投資生產,已知投資生產這兩種產品的有關數據如下表:(單位:萬美元)
兩種產品中只選擇一種進行投資生產,已知投資生產這兩種產品的有關數據如下表:(單位:萬美元)
年固定成本 | 每件產品成本 | 每件產品銷售價 | 每年最多可生產的件數 | |
A產品 | 20 |
| 10 | 200 |
B產品 | 40 | 8 | 18 | 120 |
其中年固定成本與年生產的件數無關,![]() 是待定常數,其值由生產
是待定常數,其值由生產![]() 產品的原材料決定,預計
產品的原材料決定,預計![]() ,另外,年銷售
,另外,年銷售![]() 件B產品時需上交
件B產品時需上交![]() 萬美元的特別關稅,假設生產出來的產品都能在當年銷售出去.
萬美元的特別關稅,假設生產出來的產品都能在當年銷售出去.
(1)求該廠分別投資生產A、![]() 兩種產品的年利潤
兩種產品的年利潤![]() 與生產相應產品的件數
與生產相應產品的件數![]() 之間的函數關系,并求出其定義域;
之間的函數關系,并求出其定義域;
(2)如何投資才可獲得最大年利潤?請設計相關方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知傾斜角為
中,已知傾斜角為![]() 的直線
的直線![]() 經過點
經過點![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]()
(1)寫出曲線![]() 的普通方程;
的普通方程;
(2)若直線![]() 與曲線
與曲線![]() 有兩個不同的交點
有兩個不同的交點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 滿足如下四個條件:
滿足如下四個條件:
①定義域為![]() ;
;
②![]() ;
;
③當![]() 時,
時,![]() ;
;
④對任意![]() 滿足
滿足![]() .
.
根據上述條件,求解下列問題:
⑴求![]() 及
及![]() 的值.
的值.
⑵應用函數單調性的定義判斷并證明![]() 的單調性.
的單調性.
⑶求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() ,關于x的方程[f(x)]2+mf(x)﹣1=0有三個不同的實數解,則實數m的取值范圍是( )
,關于x的方程[f(x)]2+mf(x)﹣1=0有三個不同的實數解,則實數m的取值范圍是( )
A.(﹣∞,e﹣ ![]() )
)
B.(e﹣ ![]() ,+∞)
,+∞)
C.(0,e)
D.(1,e)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地隨著經濟的發展,居民收入逐年增長,下表是該地一建設銀行連續五年的儲蓄存款(年底余額),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y (千億元) | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便,工作人員將上表的數據進行了處理,![]() 得到下表2:
得到下表2:
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)求z關于t的線性回歸方程;
(2)通過(1)中的方程,求出y關于x的回歸方程;
(3)用所求回歸方程預測到2020年年底,該地儲蓄存款額可達多少?
(附:對于線性回歸方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 右焦點
右焦點![]() ,離心率為
,離心率為![]() ,過
,過![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() ,設
,設![]() 中點分別為
中點分別為![]() .
.

(1)求橢圓的方程;
(2) 證明:直線![]() 必過定點,并求出此定點坐標;
必過定點,并求出此定點坐標;
(3) 若弦![]() 的斜率均存在,求
的斜率均存在,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com